Типы уравнений высших степеней. Старт в науке. Утверждения о корнях многочлена и его делителях
Ежегодно множество наших соотечественников получают образование за границей. Еще больше абитуриентов мечтают учиться в хороших иностранных ВУЗах, но их пугает высокая цена за образование для иностранцев. Но мы докажем, что обучение за рубежом для русских может быть бесплатным, если соблюдается несколько важных нюансов, о которых мы тоже расскажем в этой статье.
Прежде всего, стоит уточнить, что под образованием за рубежом бесплатно имеется в виду именно учебный процесс, то есть иностранец не платит только за учебу в ВУЗе. А вот питание, проживание, учебные материалы, услуги библиотеки и прочие траты в программу финансирования не входят. Поэтому перед тем, как отправиться на обучение за границу, необходимо иметь некоторую финансовую подушку на весь период учебы.
7 способов бесплатного обучения за рубежом
Главное условие обучения за границей для россиян и других иностранцев — владение международным английским языком или языком того государства, где планируется учиться. Если уровень знания языка недостаточный для того, чтобы получить бесплатное доступное обучение за рубежом, то стоит воспользоваться специальными курсами для подготовки иностранцев для поступления в заграничные учебные заведения.
Итак, есть несколько способов, как россиянин может получить зарубежное образование бесплатно. Однако все эти методы так или иначе основаны на финансовой помощи со стороны государства, частного предприятия, учебного заведения, мецената, общественной организации и т. д.
Перечислим 7 способов получения бесплатного образования за границей:
- Гранты на бесплатное обучение за рубежом 2018 или, так называемая, социальная помощь студентам от государства на реализацию профессионального проекта, образовательные расходы, прохождение курсов, повышение квалификации, обучение в летних или языковых школах и т. д. Грант выдается в виде поощрения для отличившихся студентов, единовременно, но его возможно получить еще раз.
- Стипендия от ВУЗа или государства. Отличившийся студент может быть награжден стипендией от зарубежного университета, которая покроет расходы на учебу полностью или частично. Чтобы получить стипендию, абитуриент должен написать хорошее мотивационное письмо и приложить доказательство своих заслуг перед обществом. Это может быть, творческая, волонтерская, научная, спортивная деятельность или другие достижения.
- Исследовательская стипендия. Такое поощрение, как правило, выдает заинтересованное лицо — частное или государственное предприятие, общественный фонд, которым необходим специалист в конкретной области. Исследовательская стипендия предназначена для тех, кто окончил ВУЗ и намерен в магистратуру для осуществления дальнейшей исследовательской деятельности.
- Докторантура. Еще один вид образования, которое может оплатить заинтересованное лицо — учреждение или государство. В отличие от магистратуры, студент, помимо обучения, будет трудиться ассистентом профессора: читать вводные курсы по специальности, участвовать в исследовательских проектах и т. д. Это хороший шанс получить колоссальный опыт.
- Программа «Глобальное образование». Заказчик этой программы — Министерство образования и науки РФ. За образование в другой стране платит государство, однако студент после завершения обучения обязан вернуться в Россию и отработать три года на том предприятии, которое ему определят. По этой программе можно поступить в магистратуру, аспирантуру или докторантуру за границей, а по ее окончании получить рабочее место в РФ.
- Американская программа по обмену Global UGRAD. Данная программа позволяет высшим учебным заведениям из Европы и Центральной Азии совершать обмен студентами дневной формы обучения, которые желают учиться в США. Отбор для участия в программе Global UGRAD проводится на конкурсной основе.
- Программа по обмену Au-Pair. Данная программа позволяет российским студентам учиться по обмену не только в США, но в странах Европы на срок от 4-х месяцев до 1-го года. Благодаря Au-Pair студенты получают возможность бесплатно изучать язык, знакомиться с культурой и работать за границей. Эта программа позволяет жить в семье иностранцев и посещать языковые курсы, помогая взамен «приемной» семье присматривать за детьми или вести домашнее хозяйство.
Как видите, существует немало способов бесплатно учиться в другой стране, однако перед тем, как начать готовиться к такому процессу, нужно все тщательно продумать: сколько придется тратить на питание, проживание, транспорт, какие документы потребуются, каким должен быть уровень владения языком для поступления в университет.

Куда можно поехать учиться русским бесплатно? — 10 стран
Сразу стоит отметить, что обучаться бесплатно за рубежом можно только в государственных ВУЗах, так как только такие университеты предоставляют бесплатное образование для иностранцев. В частных учебных заведениях обучение платное. Разве что между частным российским и заграничным ВУЗом есть специальное соглашение по бесплатному обмену студентами, но такое случается редко.
Перечислим, в какие страны можно поехать русским для бесплатной учебы, и какие требования для поступления они выдвигают:
- США. Студенты, которые намерены поступать в американские университеты, должны знать, что без вступительных экзаменов сделать это невозможно. Обязательное тестирование для всех абитуриентов — экзамен SAT для проверки знаний школьной программы по грамматике и математике. Кроме того, необходимо пройти тест на знание английского языка. При этом на программу «бакалавра» можно поступить после окончания школы в России, а не после окончания российского ВУЗа.
- Канада. В канадские университеты легко поступить сразу после окончания 11 классов, если, конечно, абитуриент хорошо учился на Родине. Вступительные экзамены при поступлении сдавать не нужно. Если есть сертификат, подтверждающий владение английским или французским языком, то тест на знание языка тоже проходить не надо. При поступлении в ВУЗы Канады оценивают аттестат, отдавая предпочтение тем абитуриентам, у которых высокие оценки.
- Австралия. Если россиянин свободно владеет английским языком и окончил первый курс российского ВУЗа, то он может поехать бесплатно учиться в австралийский университет. Главное — подтвердить знание языка сертификатом или прохождением языкового теста. Если же абитуриент окончил только школу, то ему сначала придется пройти обучение на нулевом подготовительном курсе, после чего уже за 3 года получить степень «бакалавра». Зато за время обучения в Австралии можно получить сразу две специальности.
- Дания. Страна с очень высоким уровнем образования, в которой широко распространены различные программы учебы по обмену. Чтобы поступить на бесплатное обучение в Данию, необходимо специальное соглашение между университетами, знание английского языка, подтвержденное сертификатом, аттестат о среднем образовании, а также справка из банка о состоянии счета для подтверждения способности оплаты проживания в этой стране.
- Австрия. Преподавание ведется на двух языках — английском или немецком. Поступить в австрийские университеты можно без вступительных тестов, но экзамен на знание одного из указанных языков пройти все же придется. Если языковой уровень недостаточный для учебы в ВУЗах Австрии, то можно пройти подготовительный курс за один учебный год, чтобы подтянуть свои знания, познакомиться с культурой и без проблем поступить в университет через год.
- Германия. Обучение тоже проходит на немецком или английском на выбор студента, также не нужны вступительные экзамены. Однако в университеты Германии иностранцев без высшего образования в родной стране не принимают. Иностранцы должны окончить хотя бы два курса университета на Родине, чтобы поступить на первый курс в Германии или закончить один курс дома, чтобы попасть на подготовительный курс в немецком ВУЗЕ.
- Бельгия. Еще одна европейская страна, позволяющая россиянам получить зарубежное образование. Преподавание ведется на английском или французском языках. Вступительное тестирование на знание школьной программы не проводится, но языковой экзамен сдается обязательно. Главный плюс — если в аттестате хорошие оценки, то можно поступить сразу после окончания школы.
- Италия. ВУЗы этой европейской страны открыты для иностранных абитуриентов, которые владеют английским или итальянским языками. Возможно поступление без экзаменов и языкового сертификата, в зависимости от наличия высшего образования и специальности. Но, как и в Германии, в итальянские университеты не поступить без окончания хотя бы 1−2 курсов российского высшего учебного заведения.
- Франция. Российских абитуриентов учебные заведения могут принимать без экзаменов сразу после того как те закончат школу. Для поступления необходим только аттестат с хорошими оценками, а также языковой сертификат либо тест на французский или английский язык.
- Финляндия. В данной стране в высшее учебное заведение студенты могут поступить только после сдачи экзаменов и языкового тестирования. Из-за того что обучение ведется либо на английском, либо на финском языке, студенты решившие поступить в ВУЗ в этой стране должны подтвердить знание языка. В колледж принимают без экзаменов.
Стоит заметить, что учебные заведения Греции, Чехии, Испании, Китая и других стран предлагают российским студентам возможность бесплатного образования. Но преподавание в ВУЗах в этом случае ведется на языке той страны, в которой он находится, т. е. китайском, чешском, испанском и так далее, а не на английском. В ВУЗы можно поступить без сдачи экзаменов сразу после окончания школы или после окончания 1 курса российского института.

Элитное образование за рубежом
Обучение за рубежом сейчас интересует всех, кто хочет получить элитное, престижное образование. Что же такое элитное образование? Как правило, это образование на высшем уровне, которое включает в себя высококвалифицированных преподавателей, высокое технологическое оснащение и другие критерии. Сегодня мы обсуждаем университеты Британии и США.

Если вас интересует обучение за рубежом, а также вы хотели бы в совершенстве овладеть английским языком, то престижные университеты и ВУЗы Великобритании и США ждут вас! Рассмотрим самые престижные зарубежные высшие учебные заведения.
Добро пожаловать в Оксфорд!
Если вас интересуют университеты Великобритании, то о них мы сейчас и поговорим. Оксфордский университет — это одна из визитных карточек Англии. Оксфорд — одно из старейших высших учебных заведений в Европе. Это один из лучших ВУЗов Англии, давший миру около 50 нобелевских лауреатов.
История этого учебного заведения удивительна. Первоначально это был монастырь, первое упоминание о котором датируется 912 годом. В 1117 было принято решение основать первый в Англии Оксфордский университет, для того, чтобы священнослужители могли получить более полное образование. И лишь при короле Генрихе II Оксфорд стал настоящим университетским городком, в котором могли учиться не только священнослужители, но и все желающие.
В последующие века короли Англии вкладывали ресурсы в развитие Оксфордской обители наук. Современный Оксфорд — это не только элитное образование, но также целый комплекс исторических и культурных достопримечательностей.
Помимо самого университета, он включает в себя колледжи Крайст-Чёрч, часовню Оксфордский собор, Колледж Магдалины, памятник поэту Шелли, Бодлианскую библиотеку, которая содержит в себе 6 миллионов книг, музей Ашмола, в котором можно увидеть произведения Леонардо Да Винчи, Рафаэля, Рембранта и других гениев живописи. Ботанический сад, крытый рынок, несколько других музеев, известные на весь мир пабы — все это можно увидеть в знаменитом Оксфорде.
Бодлианская библиотека стоит отдельного разговора. Это хранилище книг оспаривает право называться старейшим в Европе у Ватиканской библиотеки. Основатель Бодлианской библиотеки епископ Томас де Кобэм, который создал небольшое собрание книг и первоначально вынужден был приковывать их цепями к стене, чтобы книги не растащили. Спустя несколько веков это книжное хранилище взял под свое крыло сэр Томас Бодли, который превратил его в настоящую библиотеку, для этих целей приобретая книги из разных стран, включая Турцию и Китай.
Как вы можете догадаться, это не просто ВУЗ, но целый культурный городок. Он предоставляет замечательную возможность культурно развиваться и получить прекрасное элитное образование.  Престижные университеты США и Англии
Престижные университеты США и Англии
Если вас интересует Кембридж…
Продолжаем обсуждать университеты Англии, и наш разговор о том, где можно получить элитное образование и что такое обучение за рубежом , и представляем вам другой престижный ВУЗ Англии. Как вы уже догадались, конечно, это Кембридж.
Кембридж, так же, как и Оксфорд, является одним из старейших университетских центров Европы. С этим университетом связано 87 Нобелевских лауреатов. В 1214 году в Кембридже были составлены основные университетские правила. По этим правилам назначали ректора и программу с итоговыми экзаменами. Здесь стали обучать наукам, математике, философии, логике. Оксфорд и Кембридж имеют долгую историю соперничества друг с другом.
Кембридж включает в себя 31 колледж, университетскую библиотеку, обсерваторию, лабораторию. Учебная и научная деятельность организована в нескольких факультетах, по разным областям: востоковедение, английский язык, музыковедение, юриспруденция, педагогика, экономика и т. д.
Универсальная библиотека Кембриджа включает в себя не только книги, но и ноты, рукописи, рисунки, географические карты. Ежегодно ее фонды пополняются экземплярами книг и других материалов. Библиотека открыта как для преподавателей, так и для студентов.
Если вас интересует элитное образование в Кембридже, то для иностранных студентов существуют гранты, частично покрывающие стоимость обучения в Англии. Так что дерзайте!
Вы предпочли Гарвард…
Переходим на престижные университеты США. Если вас интересует Гарвардское учебное заведение в США, то это также отличная возможность получить элитное образование. Гарвард не настолько древний университет, как престижные высшие учебные заведения Англии, но и сама история США относительно новая.
Гарвардский университет был основан в 1636. Первоначально это был колледж и в нем обучались священнослужители. После гражданской войны в США Гарвард был преобразован в университет. Этот ВУЗ окончили 8 президентов США, а также 75 нобелевских лауреатов были связаны с ним, как его студенты или преподаватели.
Гарвардский университет в США включает в себя 10 факультетов: факультет медицины, богословия, стоматологии, бизнеса, дизайна и т. д. , а также Институт Перспективных Исследований Рэдклиффа.
Стоит отметить, что Институт Перспективных Исследований Рэдклиффа выделяет стипендии на конкурсной основе в рамках своей программы в различных областях знаний. Эта программа рассчитана на ученых, работающих в различных областях, а также на людей творческих профессий, таких, как художники видеографики, кино, дизайнеры звука и видео и т. д.
Все эти университеты являются престижными мировыми ВУЗами. И это не просто ВУЗы, а настоящие культурные центры США и Англии, в которых преподают знаменитые на весь мир профессоры. Жители Англии и США весьма гордятся своими старейшими учебными заведениями, позволяющими получить элитное образование.
В наше время обучение за рубежом — это реальность; вопрос только в цене обучения. В любом случае, если вас заинтересовали эти престижные университеты и вы хотите получить элитное образование, то дерзайте, у вас все получится!
Что нужно для поступления в зарубежные ВУЗы?
У каждого университета из зарубежья собственные требования к иностранным абитуриентам, но почти все они идентичны. Студенты из России могут поступить в иностранные ВУЗы, выполнив следующие требования:
- Необходимо предоставить аттестат подтверждающий окончание школы. Данное требование очень важно, так как во время приема документов первым будут рассматривать именно аттестат об окончании школы.
- Документы, в которых указаны результаты экзаменов. Обязательно нужно предоставить сертификаты ЕГЭ или ГИА. Баллы в этих документах могут существенно повлиять на то, какое решение примет комиссия.
- Для того чтобы получить второе высшее или поступить для получения степени магистра или доктора наук, необходим диплом об окончании российского университета.
- Знание английского языка. В виду того что преподавание во многих университетах ведется на английском языке, вам необходимо его знать. Базовое знание стилистики, грамматики, чтение и правописание — все это необходимо знать, чтобы пройти тестирование. Практически для каждого ВУЗа одним из главных пунктов для поступления является прохождение теста TOEFL, который проходит на компьютере.
- Возраст также имеет большое значение при поступлении. Вы должны достигнуть 18-летнего возраста.
- Сдача вступительных экзаменов. Чаще всего в ВУЗ принимают без экзаменов, но в некоторых странах Америки могут потребовать прохождение стандартного экзамена-теста SAT. Также вместо экзаменов может быть проведено собеседование по телефону или скайпу.
- Те, кто хочет поступить в магистратуру, также должны быть готовы к сдаче стандартного экзамена.
- Необходимо окончить 1−2 курса российского ВУЗа. Многие зарубежные ВУЗы могут не принять вас на 1 курс из-за того что их школьная система образования насчитывает 12 классов. В России она другая и поэтому иностранцам для поступления необходимо окончить несколько курсов родного университета.
Список документов, которые нужны для поступления в университеты за рубежом для бесплатного обучения:
- Аттестат, подтверждающий получение среднего образования.
- Диплом, свидетельствующий о получении высшего образования.
- Резюме либо автобиография по форме CV.
- Копия приложения к диплому или выписка из зачетной ведомости в том случае если документ об окончании еще не получен.
- Языковой сертификат.
- Сертификат о сдаче экзамена или теста.
- Анкета, которая заполнена согласно требованиям ВУЗа. Некоторые университеты выкладывают ее в электронном виде на сайте. Ее необходимо распечатать и подать уже заполненной в печатном виде.
- Рекомендации от кураторов, преподавателей и декана университета. Их количество от 3 до 5.
- Мотивационное письмо. Здесь вам необходимо рассказать, что вас подтолкнуло к поступлению именно в этот университет, чем вам нравится их программа обучения. Не лишним будет рассказать о своих достижениях и увлечениях, это позволит полностью раскрыть вашу личность и расположит членов комиссии.
Каждый документ имеет большое значение. В случае если не предоставить какой-либо комиссия может не зачислить вас в университет.
Полезный опыт: как украинец поступил в 10 ВУЗов США
Настоящей сенсацией в 2017 году стал студент киевского Финансово-правового лицея Георгий Солодко, который смог поступить сразу в 10 университетов США. По признанию самого студента, документы он подал в 20 лучших американских ВУЗов, но положительный ответ получил только от половины из них. Свои предложения Георгию прислали, в том числе Стэнфорд и Гарвард, но Солодко остановился на последнем, где теперь учится вместе с дочерью Обамы.
Украинскому студенту удалось получить от Гарвардского университета грант в размере 300 тысяч долларов, что полностью покрывает расходы не только на весь период обучения, но и на оплату жилья, еды, транспорта и пр. А вот авиабилеты на полеты домой, участие в различных научных конференциях и учебные материалы Георгий оплачивает сам.
На данный момент, Солодко является единственным украинцем в Грварде, однако он уверяет, что любой российский, украинский или армянский выпускник может стать стентом этого престижного университета. Чтобы это сделать, надо хорошо учиться на Родине, знать английский язык, участвовать в жизни общества, быть настойчивым, дружелюбным и иметь активную жизненную позицию.
Кроме того, подавая документы в зарубежный ВУЗ, нужно предоставить академические рекомендации от преподавателей, в которых они описывают успехи своего студента, его увлечения, рассказывают о жизненной позиции, успеваемости и лидерских качествах. Причем, просто сухой теории недостаточно: необходимо раскрывать личность своего подопечного на конкретных примерах.
Помимо рекомендаций от учителей, нужно сдать SAT — главный экзамен на знание английского языка, математики и других школьных предметов, а также TOEFL. Чем выше баллы, полученные за эти тесты, и чем выше балл в аттестате, тем больше шансов на поступление в американский ВУЗ. Сдача каждого экзамена обходится абитуриенту примерно в 100 $. Также нужно заплатить около 20 $ за отправку своих результатов в университеты.
Если у руководства университета имеются какие-то сомнения в отношении поступающего, то ему будет назначено дополнительное собеседование — интервью по Скайпу. Во время этой беседы следует соблюдать дресс-код: предстать в приличной одежде — в брюках и рубашке или пиджаке. Не стоит проходить собеседование в старой майке и шортах, попивая чай.
По словам Георгия Солодко, у него весь процесс подготовки к поступлению в зарубежные университеты занял около года. Примерно три месяца ушло на подготовку к сдаче тестов. Путь, конечно, долгий, но бесплатная учеба в престижном ВУЗе того стоит!

Марина Могилко также поступила в 5 вузов США, два из которых предоставили ей полное финансирование на магиcтратуру и MBA. Сегодня Марина предоставляет , как подготовиться и оформить документы на учебные программы в государственных вузах и стажировки за рубежом .
Многие мечтают учиться в лучших университетах мира, в которых учились многие ученые, политики, ведущие бизнесмены. Попасть в эти университеты очень сложно, а плата за обучение высокая, но нет ничего невозможного.
Мировой рынок образовательных услуг может предложить вам самые широкие возможности. Границы стран стали более прозрачными, мобильность населения повысилась, а качественное образование постоянно растет в цене.
Ранее мы уже писали о том, как пройти обучение в лучших университетах Азии. Относительно невысокая цена и прекрасные программы привлекают в них массу иностранных студентов.
Но существует ряд университетов, одно упоминание о которых вызывает непроизвольное желание начать учебу. Они занимают высшие строчки мировых университетских рейтингов, их названия уже давно стали крупнейшими брендами, а успешное завершение этих образовательных учреждений гарантирует прекрасные перспективы. «РБК.Личные финансы» расскажут о лучших университетах мира и о том, как туда попасть.
Принстон
Принстонский университет был основан еще в 1746 году и входит в список так называемых колониальных колледжей, которые были основаны еще до Американской революции. Принстон – целый городок с большим числом корпусов и зданий. А университетская библиотека содержит более 7 млн книг. Важно отметить, что Принстон является частным учебным заведением.
Учебный процесс в Принстонском университете разделен на два потока. Студенты могут посвятить себя искусству или естественным наукам. Тем не менее базовые дисциплины, в числе которых литература, история, этика и мораль, иностранный язык, естествознание, обязательны для каждого. Те, кто претендует на степень бакалавра искусств, должны прослушать один курс писательского мастерства.
На третьем курсе студент пишет исследовательские работы, а на четвертом – дипломную работу. Причем некоторые факультеты предоставляют возможность подойти к дипломной работе с творческой стороны. Например, обучение на литературном факультете подразумевает написание романа. А выпускники факультета визуальных искусств ставят спектакль. Иностранец, который желает здесь обучаться, должен пройти экзамен TOEFL. Также приемная комиссия будет довольна, если вы занимаетесь творческой деятельностью – посещаете театральный кружок, танцуете, поете или рисуете.
Интересно, что комиссия оценивает не только формальные достижения абитуриента (оценки), но и индивидуальные успехи. Поэтому любой опыт работы или общественной деятельности будет плюсом. Один год обучения в Принстонском университете обойдется в 1 млн 700 тыс. руб. В цену входит проживание в общежитии.
Гарвард
Самый старый университет Соединенных Штатов на данный момент окончили восемь президентов. Среди них – последний глава США Барак Обама . Также Гарвард занимает первое место в стране по числу миллиардеров среди выпускников. Система образования схожа с Принстонским университетом. Студенты получают широкое базовое образование и на выходе могут похвастаться дипломом бакалавра искусств или наук. Они живут в общежитии, а за особые успехи в обучении их поселяют в так называемых домах, которых в университете двенадцать.
Эти дома выполняют не только жилые функции, но и административные. Здесь проводятся собрания, в которых старшие студенты помогают адаптироваться новеньким к учебному процессу.
В Гарвардский университет можно поступить с 17 лет. Разумеется, нужно иметь отличные оценки в школьном аттестате и успешно пройти вступительные испытания, которые представляют из себя тесты на знание тех дисциплин, которые лягут в основу будущей специализации. Примечательно, что сертификат, подтверждающий знание английского, не требуется. Один год обучения будет стоить примерно 1,5 млн руб. в зависимости от выбранного факультета и других небольших расходов.
Оксфорд
Первый университет Великобритании уже давно стал легендарным. Высочайшее качество образования обеспечивается мощным преподавательским корпусом, возможностью заниматься практическими исследованиями (здесь расположен крупнейший научно-исследовательский институт) и атмосферой настоящего учебного заведения, где люди стремятся проявить свои лучшие качества и узнать как можно больше. Более двадцати премьер-министров Великобритании были выпускниками Оксфорда.
Интересно, что поступать в Оксфорд можно в любом возрасте. Еще одна забавная деталь. Вы не сможете одновременно подать документы и в Оксфорд, и в Кембридж. Два этих британских университета издавна конкурируют между собой.
Также стоит отметить, что в Оксфорде есть отделение изучения России и Восточной Европы. Помимо этого отделения здесь есть большое число других. Студенты знакомятся с огромным количеством дисциплин – от классической литературы и музыки до физики и археологии. Есть и медицинские отделения, где изучают неврологию, фармакологию и генетику. В принципе здесь можно найти занятие себе по душе.
Заявление нужно подавать через единую британскую службу UCAS, которая, по сути, является общегосударственной приемной комиссией. В анкете нужно указать, что вы хотите получить образование в Оксфорде. Требования для абитуриента стандартные. Во-первых, отличное знание английского языка. Во-вторых, хороший вступительный балл по итогам различных тестов. Год обучения в Оксфордском университете стоит 1,5 млн руб.
Гарвард и Стэнфорд по праву считаются наиболее престижными бизнес-школами в мире. Здесь можно пройти лучшие программы MBA за рубежом.
Основательная - лишь один из этапов поступления в бизнес-школу вашей мечты. Так как же определить, какая программа лучше всего подходит для вас?
Результаты анализа учебных планов MBA
Зарубежные исследователи проанализировали учебные планы MBA, рейтинги, а также сильные и слабые стороны обучения в каждом из университетов и пришли к следующим выводам.
- В Гарварде будет интереснее учиться тем студентам, которые желают получить знания в области экономики и бизнеса; в Стэнфорде - студентам, склонным к гуманитарным наукам.
- В Гарварде студентам предоставляется больше времени на самостоятельную подготовку. В Стэнфорде уровень взаимодействия между студентами и преподавателями более высокий.
- Стэнфорд находится в самом сердце Силиконовой долины, в нескольких минутах езды от крупнейших мировых компаний. Гарвард находится в Бостоне - одном из привлекательнейших городов Америки.
- Программа обучения MBA и в Гарварде, и в Стэнфорде составляет 2 года. Однако в самих программах есть некоторые различия.
- В Гарвардской бизнес-школе широко распространены методы тематических исследований, кейс-методы, командные проекты. Студенты принимают участие в анализе конкретных ситуаций и решении реальных задач в области экономики и бизнеса.
- Студенты Стэнфорда получают знания и практический опыт, работая, как правило, в течение нескольких недель в какой-либо фирме или участвуя в программе по обмену с университетом Цинхуа в Китае (программа STEP). Учебный план Стэнфорда считается более гибким. В Гарварде - сам процесс обучения считается более интенсивным.
- Выпускники Гарварда работают, как правило, в финансовых и консалтинговых отраслях; выпускники Стэнфорда - в отраслях промышленности, финансов и технологий.
Так что же выбрать?
Куда бы вы ни поступали, в Гарвард или Стэнфорд, хороший поможет вам достичь цели.
С точки зрения престижа, они оба имеют хорошую репутацию. В обеих школах вы будете окружены действительно интересными людьми. Так что речь идет не о лучшей школе, но о том, какая школа подходит именно для вас.
«Методы решения уравнений высших степеней»
( Киселёвские чтения )
Учитель математики Афанасьева Л.А
МКОУ Верхнекарачанская СОШ
Грибановского района, Воронежской области
2015 год
Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека.
Известный немецкий математик Курант писал: «На протяжении двух с лишним тысячелетий обладание некоторыми, не слишком поверхностными, знаниями в области математики входило необходимой составной частью в интеллектуальный инвентарь каждого образованного человека». И среди этих знаний не последнее место принадлежит умению решать уравнения.
Уже в древности люди осознали, как важно научиться решать алгебраические уравнения. Около 4000 лет назад вавилонские ученые владели решением квадратного уравнения и решали системы двух уравнений, из которых одно – второй степени. С помощью уравнений решались разнообразные задачи землемерия, архитектуры и военного дела, к ним сводились многие и разнообразные вопросы практики и естествознания, так как точный язык математики позволяет просто выразить факты и соотношения, которые, будучи изложенными обычным языком, могут показаться запутанными и сложными. Уравнение одно из важнейших понятий математики. Развитие методов решения уравнений, начиная с зарождения математики как науки, долгое время было основным предметом изучения алгебры. И сегодня на уроках математики, начиная с первой ступени обучения, решению уравнений различных видов уделяется большое внимание.
Универсальной формулы для нахождения корней алгебраического уравнения n – ой степени нет. Многим, разумеется, приходила в голову заманчивая мысль найти для любой степени n формулы, которые выражали бы корни уравнения через его коэффициенты, то есть, решали бы уравнение в радикалах. Однако «мрачное средневековье» оказалось как нельзя более мрачным и в отношении обсуждаемой задачи – в течение целых семи столетий требуемых формул никто не нашёл! Только в 16 веке итальянским математикам удалось продвинуться дальше – найти формулы для n =3 и n =4 . Одновременно вопросом об общем решении уравнений 3-й степени занимались Сципион Даль Ферро, его ученик Фиори и Тарталья. В 1545 году вышла книга итальянского математика Д Кардано «Великое искусство, или О правилах алгебры», где наряду с другими вопросами алгебры рассматриваются общие способы решения кубических уравнений, а так же метод решения уравнений 4 – й степени, открытый его учеником Л. Феррари. Полное изложение вопросов, связанных с решением уравнений 3-й 4-й степеней, дал Ф. Виет. А в 20-х годах 19 века норвежский математик Н. Абель доказал, что корни уравнений 5-й и более высоких степеней не могут быть выражены через радикалы.
Процесс отыскания решений уравнения заключается обычно в замене уравнения равносильным. Замена уравнения равносильным основана на применении четырёх аксиом:
1. Если равные величины увеличить на одно и то же число, то результаты будут равны.
2. Если из равных величин вычесть одно и то же число, то результаты будут равны.
3. Если равные величины умножить на одно и то же число, то результаты будут равны.
4. Если равные величины разделить на одно и то же число, то результаты будут равны.
Поскольку левая часть уравнения Р(х) = 0 представляет собой многочлен n-й степени, то полезно напомнить следующие утверждения:
Утверждения о корнях многочлена и его делителях:
1. Многочлен n-й степени имеет число корней не превышающее число n, причем корни кратности m встречаются ровно m раз.
2. Многочлен нечетной степени имеет хотя бы один действительный корень.
3. Если α – корень Р(х), то Р n (х) = (х — α)·Q n — 1 (x), где Q n — 1 (x) – многочлен степени (n – 1).
4. Всякий целый корень многочлена с целыми коэффициентами является делителем свободного члена.
5. Приведенный многочлен с целыми коэффициентами не может иметь дробных рациональных корней.
6. Для многочлена третьей степени
Р 3 (х) = ах 3 + bx 2 + cx + d возможно одно из двух: либо он разлагается в произведение трех двучленов
Р 3 (x) = а (х — α)(х — β)(х — γ), либо разлагается в произведение двучлена и квадратного трехчлена Р 3 (x) = а(х — α)(х 2 + βх + γ).
7. Любой многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов.
8. Многочлен f (x) делится на многочлен g(х) без остатка, если существует многочлен q(x), что f(x) = g(x)·q(x). Для деления многочленов применяется правило «деления уголком».
9. Для делимости многочлена P(x) на двучлен (x – c) необходимо и достаточно, чтобы с было корнем P(x) (Следствие теоремы Безу).
10. Теорема Виета: Если х 1 , х 2 , …, х n – действительные корни многочлена
Р(х) = а 0 х n + а 1 х n — 1 + … + а n , то имеют место следующие равенства:
х 1 + х 2 + … + х n = -а 1 /а 0 ,
х 1 · х 2 + х 1 · х 3 + … + х n — 1 · х n = a 2 /а 0 ,
х 1 · х 2 · х 3 + … + х n — 2 · х n — 1 · х n = -a 3 /а 0 ,
х 1 · х 2 · х 3 · х n = (-1) n a n /а 0 .
Решение примеров
Пример 1 . Найти остаток от деления Р(х) = х 3 + 2/3 x 2 – 1/9 на (х – 1/3).
Решение. По следствию из теоремы Безу: «Остаток от деления многочлена на двучлен (х — с) равен значению многочлена от с». Найдем Р(1/3) = 0. Следовательно, остаток равен 0 и число 1/3 – корень многочлена.
Ответ: R = 0.
Пример 2 . Разделить «уголком» 2х 3 + 3x 2 – 2х + 3 на (х + 2). Найти остаток и неполное частное.
Решение:
2х 3 + 3x 2 – 2х + 3| х + 2
2х 3 + 4x 2 2x 2 – x
X 2 – 2x
X 2 – 2x
Ответ: R = 3; частное: 2х 2 – х.
Основные методы решения уравнений высших степеней
1. Введение новой переменной
Метод введения новой переменной заключается в том, что для решения уравнения f(x) = 0 вводят новую переменную (подстановку) t = x n или t = g(х) и выражают f(x) через t, получая новое уравнение r(t). Решая затем уравнение r(t), находят корни: (t 1 , t 2 , …, t n). После этого получают совокупность n уравнений q(x) = t 1 , q(x) = t 2 , … , q(x) = t n , из которых находят корни исходного уравнения.
Пример; (х 2 + х + 1) 2 – 3х 2 — 3x – 1 = 0.
Решение: (х 2 + х + 1) 2 – 3х 2 — 3x – 1 = 0.
(х 2 + х + 1) 2 – 3(х 2 + x + 1) + 3 – 1 = 0.
Замена (х 2 + х + 1) = t.
t 2 – 3t + 2 = 0.
t 1 = 2, t 2 = 1. Обратная замена:
х 2 + х + 1 = 2 или х 2 + х + 1 = 1;
х 2 + х — 1 = 0 или х 2 + х = 0;
Из первого уравнения: х 1, 2 = (-1 ± √5)/2, из второго: 0 и -1.
Метод введения новой переменной находит применение при решении возвратных уравнений, то есть уравнений вида а 0 х n + а 1 х n – 1 + .. + а n – 1 х + а n =0, в котором коэффициенты членов уравнения, одинаково отстоящих от начала и конца, равны.
2. Разложение на множители методом группировки и формул сокращенного умножения
Основа данного метода заключается в группировке слагаемых таким образом, чтобы каждая группа содержала общий множитель. Для этого иногда приходится применять некоторые искусственные приемы.
Пример: х 4 — 3x 2 + 4х – 3 = 0.
Решение. Представим — 3x 2 = -2x 2 – x 2 и сгруппируем:
(х 4 — 2x 2) – (x 2 — 4х + 3) = 0.
(х 4 — 2x 2 +1 – 1) – (x 2 — 4х + 3 + 1 – 1) = 0.
(х 2 – 1) 2 – 1 – (x – 2) 2 + 1 = 0.
(х 2 – 1) 2 – (x – 2) 2 = 0.
(х 2 – 1 – х + 2)(х 2 – 1 + х — 2) = 0.
(х 2 – х + 1)(х 2 + х — 3) = 0.
х 2 – х + 1 = 0 или х 2 + х — 3 = 0.
В первом уравнении нет корней, из второго: х 1, 2 = (-1 ± √13)/2.
3. Разложение на множители методом неопределенных коэффициентов
Суть метода состоит в том, что исходный многочлен раскладывается на множители с неизвестными коэффициентами. Используя свойство, что многочлены равны, если равны их коэффициенты при одинаковых степенях, находят неизвестные коэффициенты разложения.
Пример: х 3 + 4x 2 + 5х + 2 = 0.
Решение. Многочлен 3-й степени можно разложить в произведение линейного и квадратного множителей.
х 3 + 4x 2 + 5х + 2 = (х — а)(x 2 + bх + c),
х 3 + 4x 2 + 5х + 2 = х 3 +bx 2 + cх — ax 2 — abх — ac,
х 3 + 4x 2 + 5х + 2 = х 3 + (b – a)x 2 + (c – ab)х – ac.
Решив систему:
получим
х 3 + 4x 2 + 5х + 2 = (х + 1)(x 2 + 3х + 2).
Корни уравнения (х + 1)(x 2 + 3х + 2) = 0 находятся легко.
Ответ: -1; -2.
4. Метод подбора корня по старшему и свободному коэффициенту
Метод опирается на применение теорем:
1) Всякий целый корень многочлена с целыми коэффициентами является делителем свободного члена.
2) Для того, чтобы несократимая дробь p/q (p – целое, q — натуральное) была корнем уравнения с целыми коэффициентами, необходимо, чтобы число p было целым делителем свободного члена а 0 , а q – натуральным делителем старшего коэффициента.
Пример: 6х 3 + 7x 2 — 9х + 2 = 0.
Решение:
2: p = ±1, ±2
6: q = 1, 2, 3, 6.
Следовательно, p/q = ±1, ±2, ±1/2, ±1/3, ±2/3, ±1/6.
Найдя один корень, например – 2, другие корни найдем, используя деление уголком, метод неопределенных коэффициентов или схему Горнера.
Ответ: -2; 1/2; 1/3.
5. Графический метод.
Данный метод состоит в построении графиков и использовании свойств функций.
Пример: х 5 + х – 2 = 0
Представим уравнение в виде х 5 = — х + 2. Функция у = х 5 является возрастающей, а функция у = — х + 2 — убывающей. Значит, уравнение х 5 + х – 2 = 0 имеет единственный корень -1.
6.Умножение уравнения на функцию.
Иногда решение алгебраического уравнения существенно облегчается, если умножить обе его части на некоторую функцию – многочлен от неизвестной. При этом надо помнить, что возможно появление лишних корней – корней многочлена, на который умножили уравнение. Поэтому надо либо умножать на многочлен, не имеющий корней, и получить равносильное уравнение, либо умножать на многочлен, имеющий корни, и тогда каждый из таких корней надо обязательно подставить в исходное уравнение и установить, является ли это число его корнем.
Пример. Решить уравнение:
X 8 – X 6 + X 4 – X 2 + 1 = 0. (1)
Решение: Умножив обе части уравнения на многочлен Х 2 + 1, не имеющий корней, получим уравнение:
(Х 2 +1) (Х 8 – Х 6 + Х 4 – Х 2 + 1) = 0 (2)
равносильное уравнению (1). Уравнение (2) можно записать в виде:
Х 10 + 1= 0 (3)
Ясно, что уравнение (3) не имеет действительных корней, поэтому уравнение (1) их не имеет.
Ответ: нет решений.
Кроме названных методов решения уравнений высших степеней существуют и другие. Например, выделение полного квадрата, схема Горнера, представление дроби в виде двух дробей. Из общих методов решения уравнений высших степеней, которые встречаются чаще всего, используют: метод разложения левой части уравнения на множители;
метод замены переменной (метод введения новой переменной); графический способ. С этими методами мы знакомим учащихся 9 класса при изучении темы «Целое уравнение и его корни». В учебнике Алгебра 9 (авторы Макарычев Ю.Н., Миндюк Н.Г и др) последних годов издания достаточно подробно рассматриваются основные методы решения уравнений высших степеней. Кроме этого в разделе «Для тех, кто хочет знать больше», на мой взгляд, доступно излагается материал о применении теорем о корне многочлена и целых корнях целого уравнения при решении уравнений высших степеней. Хорошо подготовленные ученики с интересом изучают этот материал, а затем представляют одноклассникам решённые уравнения.
Практически всё, что окружает нас, связано в той или иной мере с математикой. А достижения в физике, технике, информационных технологиях только подтверждают это. И что очень важно – решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF
Введение
Решение алгебраических уравнений высших степеней с одним неизвестным представляет собой одну из труднейших и древнейших математических задач. Этими задачами занимались самые выдающиеся математики древности.
Решение уравнений n-ой степени является важной задачей и для современной математики. Интерес к ним достаточно велик, так как эти уравнения тесно связаны с поиском корней уравнений, не рассматриваемых школьной программой по математике.
Проблема: отсутствие навыков решения уравнений высших степеней различными способами у учащихся мешает им успешно подготовиться к итоговой аттестации по математике и математическим олимпиадам, обучению в профильном математическом классе.
Перечисленные факты определили актуальность нашей работы «Решение уравнений высших степеней».
Владение простейшими способами решения уравнений n-ой степени сокращает время для выполнения задания, от которого зависит результат работы и качество процесса обучения.
Цель работы: изучение известных способов решения уравнений высших степеней и выявление наиболее доступных из них для практического применения.
Исходя из поставленной цели, в работе определены следующие задачи:
Изучить литературу и Интернет-ресурсы по данной теме;
Познакомиться с историческими фактами, касающимися данной темы;
Описать различные способы решения уравнений высших степеней
сравнить степень сложности каждого из них;
Познакомить одноклассников со способами решения уравнений высших степеней;
Создать подборку уравнений для практического применения каждого из рассмотренных способов.
Объект исследования - уравнения высших степеней с одной переменной.
Предмет исследования - способы решения уравнений высших степеней.
Гипотеза: общего способа и единого алгоритма, позволяющего за конечное число шагов находить решения уравнений n-ой степени, не существует.
Методы исследования:
- библиографический метод (анализ литературы по теме исследования);
- метод классификации;
- метод качественного анализа.
Теоретическая значимость исследования состоит в систематизации способов решения уравнений высших степеней и описании их алгоритмов.
Практическая значимость - предъявленный материал по данной теме и разработка учебного пособия для учащихся по данной теме.
1.УРАВНЕНИЯ ВЫСШИХ СТЕПЕНЕЙ
1.1 Понятие уравнения n-ой степени
Определение 1. Уравнением n-ой степени называется уравнение вида
a 0 xⁿ+a 1 x n -1 +a 2 xⁿ - ²+…+a n -1 x+a n = 0, где коэффициенты a 0, a 1, a 2…, a n -1, a n- любые действительные числа, причём,a 0 ≠ 0 .
Многочлен a 0 xⁿ+a 1 x n -1 +a 2 xⁿ - ²+…+a n -1 x+a n называют многочленом n-ой степени. Коэффициенты различают по названиям: a 0 - старший коэффициент; a n- свободный член.
Определение 2. Решениями или корнями для данного уравнения являются все значения переменной х , которые обращают это уравнение в верное числовое равенство или, при котором многочлен a 0 xⁿ+a 1 x n -1 +a 2 xⁿ - ²+…+a n -1 x+a n обращается в нуль. Такое значение переменной х называют также корнем многочлена. Решить уравнение - это значит найти все его корни или установить, что их нет.
Если a 0 = 1, то такое уравнение называют приведенным целым рациональным уравнением n-й степени.
Для уравнений третьей и четвёртой степени существуют формулы Кардано и Феррари, выражающими корни этих уравнений через радикалы. Выяснилось, что на практике ими редко пользуются. Таким образом, если n ≥ 3, а коэффициенты многочлена произвольные действительные числа, то поиск корней уравнения − задача непростая. Тем не менее, во многих частных случаях эта задача решается до конца. Остановимся на некоторых из них.
1.2 Исторические факты решения уравнений высших степеней
Уже в древности люди осознали, как важно научиться решать алгебраические уравнения. Около 4000 лет назад вавилонские ученые владели решением квадратного уравнения и решали системы двух уравнений, из которых одно - второй степени. С помощью уравнений высших степеней решались разнообразные задачи землемерия, архитектуры и военного дела, к ним сводились многие и разнообразные вопросы практики и естествознания, так как точный язык математики позволяет просто выразить факты и соотношения, которые, будучи изложенными обычным языком, могут показаться запутанными и сложными.
Универсальной формулы для нахождения корней алгебраического уравнения n-ой степени нет. Многим, разумеется, приходила в голову заманчивая мысль найти для любой степени n формулы, которые выражали бы корни уравнения через его коэффициенты, то есть, решали бы уравнение в радикалах.
Только в 16 веке итальянским математикам удалось продвинуться дальше - найти формулы для n= 3 и n= 4. Одновременно вопросом об общем решении уравнений 3-й степени занимались Сципион, Даль, Ферро и его ученики Фиори и Тарталья.
В 1545 году вышла книга итальянского математика Д. Кардано «Великое искусство, или о правилах алгебры», где наряду с другими вопросами алгебры рассматриваются общие способы решения кубических уравнений, а также метод решения уравнений 4-й степени, открытый его учеником Л. Феррари .
Полное изложение вопросов, связанных с решением уравнений 3-й и 4-й степеней, дал Ф. Виет.
В 20-х годах 19 века, норвежский математик Н. Абель доказал, что корни уравнений пятой степени не могут быть выражены через радикалы .
В ходе исследования было выявлено, что современной науке известно множество способов решения уравнений n-ой степени.
Результатом поиска методов решения уравнений высших степеней, неподдающихся решению способами, рассматриваемыми в школьной программе, стали способы, основанные на применении теоремы Виета (для уравнений степени n>2 ), теоремы Безу, схемы Горнера, а также формула Кардано и Феррари для решения кубических уравнений и уравнений четвертой степени.
В работе представлены методы решения уравнений и их виды, которые для нас стали открытием. К ним можно отнести - метод неопределенных коэффициентов, выделение полной степени, симметрические уравнения.
2. РЕШЕНИЕ ЦЕЛЫХ УРАВНЕНИЙ ВЫСШИХ СТЕПЕНЕЙ С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ
2.1 Решение уравнений 3-ей степени. Формула Д. Кардано
Рассмотрим уравнения вида x 3 +px+q=0. Преобразуем уравнение общего вида к виду: x 3 +px 2 +qx+r=0. Запишем формулу куба суммы; Сложим с первоначальным равенством и заменим на y . Получим уравнение: y 3 + (q -) (y -) + (r - =0. После преобразований, имеем: y 2 +py + q=0. Теперь, снова запишем формулу куба суммы:
(a + b ) 3 =a 3 + 3a 2 b + 3ab 2 + b 3 = a 3 + b 3 + 3ab (a + b), заменим (a + b )на x , получим уравнение x 3 - 3abx - (a 3 +b 3) = 0. Теперь видно, что исходное уравнение равносильно системе: и Решая систему, получим:
Мы получили формулу для решения приведенного уравнения 3-й степени. Она носит имя итальянского математика Кардано.
Рассмотрим пример. Решить уравнение: .
Имеем р = 15 и q = 124, тогда используя формулу Кардано вычислим корень уравнения
Вывод: данная формула хороша, но не подходит для решения всех кубических уравнений. Вместе с тем она громоздка. Поэтому на практике ею пользуются редко.
Но тот, кто овладеет данной формулой, может использовать её при решении уравнений третьей степени на ЕГЭ.
2.2 Теорема Виета
Из курса математики мы знаем данную теорему для квадратного уравнения, но мало кто знает, что ее используют и для решения уравнений высших степеней.
Рассмотрим уравнение:
разложим левую часть уравнения на множители, разделим на ≠ 0.
Правую часть уравнения преобразуем к виду
; отсюда следует, можно записать в систему следующие равенства:
Формулы, выведенные Виетом для квадратных уравнений и продемонстрированные нами для уравнений 3-й степени, верны и для многочленов высших степеней.
Решим кубическое уравнение:
Вывод: данный способ универсален и достаточно легок для понимания учащимися, так как теорема Виета им знакома по школьной программе для n = 2. Вместе с тем, чтобы находить корни уравнений с помощью данной теоремы необходимо обладать хорошими вычислительными навыками.
2.3 Теорема Безу
Эта теорема, названа по имени французского математика XVIII века Ж. Безу.
Теорема. Если уравнение a 0 xⁿ+a 1 x n -1 +a 2 xⁿ - ²+…+a n -1 x+a n = 0, в котором все коэффициенты целые числа, причем свободный член отличен от нуля, имеет целый корень, то этот корень является делителем свободного члена.
Учитывая, что в левой части уравнения многочлен n-й степени, то теорема имеет и другую трактовку.
Теорема. При делении многочлена n-й степени относительно x на двучлен x - a остаток равен значению делимого при x = a . (буква a может обозначать любое действительное или мнимое число, т.е. любое комплексное число) .
Доказательство: пусть f(x ) обозначает собой произвольный многочлен n-й степени относительно переменной x и пусть при его делении на двучлен (x-a ) получилось в частном q(x ), а в остатке R . Очевидно, что q(x) будет некоторый многочлен (n- 1)-й степени относительно x , а остаток R будет величиной постоянной, т.е. не зависящей от x .
Если бы остаток R был многочленом первой степени относительно x, то это означало бы, что деление не выполнено. Итак, R от x не зависит. По определению деления получаем тождество: f(x)=(x-a) q(x)+R .
Равенство справедливо при всяком значении x, значит, оно справедливо и при x=a , получим: f(a)=(a-a) q(a)+R . Символ f(a ) обозначает собой значение многочлена f(x ) при x=a, q(a) обозначает значение q(x ) при x=a. Остаток R остался таким, каким он был раньше, так как R от x не зависит. Произведение (x-a) q(a) = 0 , так как множитель (x-a) = 0, а множитель q(a) есть определенное число. Поэтому из равенства получим: f(a)= R, ч.т.д.
Пример 1. Найти остаток от деления многочлена x 3 - 3x 2 + 6x- 5 на двучлен
x- 2. По теореме Безу: R=f (2) = 23-322 + 62 -5=3. Ответ: R= 3.
Отметим, что теорема Безу важна не столь сама по себе, сколько своими следствиями. (Приложение 1)
Остановимся на рассмотрении некоторых приемов применения теоремы Безу к решению практических задач. Следует отметить, что при решении уравнений с помощью теоремы Безу необходимо:
Найти все целые делители свободного члена;
Из этих делителей найти хотя бы один корень уравнения;
Левую часть уравнения разделить на (х-а );
Записать в левой части уравнения произведение делителя и частного;
Решить полученное уравнение.
Рассмотрим на примере решения уравнения х 3 + 4х 2 + х - 6 = 0 .
Решение:находим делители свободного члена ±1; ± 2; ± 3; ± 6. Вычислим значения при х= 1, 1 3 + 41 2 + 1- 6=0. Разделим левую часть уравнения на (х- 1). Деление выполним «уголком», получим:
Вывод: теорема Безу один из тех способов, которые мы рассматриваем в нашей работе, изучается в программе факультативных занятий. Она трудна в понимании, потому что, чтобы ей владеть, надо знать все следствия из нее, но при этом теорема Безу является одним из главных помощников учащихся на ЕГЭ.
2.4 Схема Горнера
Для деления многочлена на двучлен х-α можно использовать специальный несложный прием, придуманный английскими математиками XVII века, впоследствии названной схемой Горнера. Помимо нахождения корней уравнений, по схеме Горнера можно более просто вычислять их значения. Для этого необходимо подставить значение переменной в многочлен Pn(x)=a 0 xn+a 1 x n-1 +a 2 xⁿ - ²+…++ a n -1 x+a n. (1)
Рассмотрим деление многочлена (1) на двучлен x -α.
Выразим коэффициенты неполного частного b 0 xⁿ - ¹+ b 1 xⁿ - ²+ b 2 xⁿ - ³+…+ bn -1 и остаток r через коэффициенты многочлена Pn(x ) и число α. b 0 =a 0 , b 1 = α b 0 +a 1 , b 2 = α b 1 +a 2 …, bn -1 =
= α bn -2 +a n -1 = α bn -1 +a n .
Вычисления по схеме Горнера представлены в виде следующей таблицы:
|
а 0 |
a 1 |
a 2 , |
|||
|
b 0 =а 0 |
b 1 = α b 0 +a 1 |
b 2 = α b 1 +a 2 |
r=α b n-1 +a n |
Поскольку r=Pn(α), то α − корень уравнения. Для того чтобы проверить не является ли α кратным корнем, схему Горнера можно применить уже к частному b 0 x+ b 1 x+…+ bn -1 по таблице. Если в столбце под bn -1 получится снова 0, значит α − кратный корень.
Рассмотрим пример: решить уравнение х 3 + 4х 2 + х - 6 = 0.
Применим к левой части уравнения разложение на множители многочлена, стоящего в левой части уравнения, схему Горнера.
Решение:находим делители свободного члена ± 1; ± 2; ± 3; ± 6.
|
6 ∙ 1 + (-6) = 0 |
Коэффициенты частного - числа 1, 5, 6, а остаток r = 0.
Значит, х 3 + 4х 2 + х - 6 = (х - 1) (х 2 + 5х + 6) = 0.
Отсюда: х - 1 = 0 или х 2 + 5х + 6 = 0.
х = 1, х 1 = -2; х 2 = -3. Ответ: 1,- 2, - 3.
Вывод: таким образом, на одном уравнении мы показали применение двух различных способов разложения на множители многочленов. На наш взгляд, схема Горнера наиболее практична и экономична.
2.5 Решение уравнений 4-ой степени. Метод Феррари
Ученик Кардано Людовик Феррари обнаружил способ решения уравнения 4-й степени. Метод Феррари состоит из двух этапов.
I этап: уравнения вида представляется в виде произведения двух квадратных трехчленов это следует из того, что уравнение 3-ей степени и хотя бы одно решение.
II этап: полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.
Идея в том, чтобы представить уравнения в виде A 2 =B 2 , где A=x 2 +s,
B-линейная функция от x . Тогда остаётся решить уравнения A = ±B.
Для наглядности рассмотрим уравнение: Уединим 4-ю степень, получим: Для любого d выражение будет полным квадратом. Прибавим к обеим частям уравнения получим
В левой части полный квадрат, можно подобрать d , чтобы и правая часть (2) стала полным квадратом. Представим себе, что мы достигли этого. Тогда наше уравнение выглядит так:
Найти корень впоследствии не составит никакого труда. Чтобы правильно подобрать d надо, чтобы дискриминант правой части (3) обратился в нуль, т.е.
Итак, чтобы найти d , надо решить это уравнение 3-й степени. Такое вспомогательное уравнение называют резольвентой .
Легко находим целый корень резольвенты: d = 1
Подставив в (1) уравнение получим
Вывод: метод Феррари универсален, но сложен и громоздкий. Вместе с тем, если алгоритм решения понятен, то уравнения 4-й степени можно решать данным методом.
2.6 Метод неопределенных коэффициентов
Успех решения уравнения 4-й степени методом Феррари зависит от того, реши ли мы резольвенту - уравнение 3-й степени, что как мы знаем, не всегда удается.
Суть метода неопределенных коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определяется путем перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной .
Пример: решите уравнение:
Предположим, что левую часть нашего уравнения можно разложить на два квадратных трехчлена с целыми коэффициентами такие, что справедливо тождественное равенство
Очевидно, что коэффициенты перед уних должны быть равными 1, а свободные члены - у одного + 1, у другого - 1.
Неопределенными остаются коэффициенты, стоящие перед х . Обозначим их через а и и чтобы их определить, перемножим оба трехчлена правой части уравнения.
В результате получим:
Приравнивая коэффициенты при одинаковых степенях х в левой и правой частях равенства (1), получаем систему для нахождения и
Решив эту систему, будем иметь
Итак, наше уравнение равносильно уравнению
Решив его, получаем следующие корни: .
Метод неопределенных коэффициентов опирается на следующие утверждения: любой многочлен четвертой степени, стоящий в уравнении, можно разложить на произведение двух многочленов второй степени; два многочлена тождественно равны тогда и только тогда, когда равны их коэффициенты при одинаковых степенях х.
2.7 Симметрические уравнения
Определение. Уравнение вида называется симметрическим, еслипервые коэффициенты, стоящие в уравнении слева, равны первым коэффициентам, стоящим справа .
Мы видим, что первые коэффициенты слева равны первым коэффициентам справа.
Если такое уравнение имеет нечетную степень, то оно имеет корень х = - 1. Далее мы можем понизить степень уравнения, поделив его на (х+ 1). Оказывается, что при делении симметрического уравнения на (х+ 1) получается симметрическое уравнение четной степени. Доказательство симметричности коэффициентов представлено ниже. (Приложение 6) Наша задача - научиться решать симметрические уравнения четной степени.
Например: (1)
Решим уравнение (1), поделим на х 2 (на среднюю степень) = 0.
Сгруппируем слагаемые с симметричными
) + 3(x + . Обозначим у = x + , возведём обе части в квадрат, отсюда = у 2 Итак, 2(у 2 или 2у 2 + 3 решив уравнение, получим у = , у = 3. Далее вернёмся к замене x + = и x + = 3. Получим уравнения и Первое не имеет решения, а второе имеет два корня. Ответ:.
Вывод: данный вид уравнений не часто встречающийся, но если он вам попался, то его можно решить легко и просто не прибегая к громоздким вычислениям.
2.8 Выделение полной степени
Рассмотрим уравнение.
Левая часть представляет собой куб суммы (х+1), т.е.
Извлекаем корень третьей степени из обеих частей: , далее получим
Откуда единственный корень.
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ
По результатам работы мы пришли к следующим выводам:
Благодаря изученной теории мы познакомились с различными методами решения целых уравнений высших степеней;
Формула Д. Кардано является сложной в применении и даёт большую вероятность допустить ошибки при вычислении;
− метод Л. Феррари позволяет свести решение уравнения четвертой степени к кубическому;
− теорема Безу может применяться как для кубических уравнений, так и для уравнений четвертой степени; она более понятна и наглядна в применении к решению уравнений;
Схема Горнера помогает существенно сократить и упростить вычисления в решении уравнений. Помимо нахождения корней, по схеме Горнера можно более просто вычислять значения многочленов, стоящих в левой части уравнения;
Особый интерес вызвали решения уравнений методом неопределённых коэффициентов, решение симметрических уравнений.
В ходе исследовательской работы было выяснено, что с простейшими способами решения уравнений высшей степени учащиеся знакомятся на занятиях факультатива по математике, начиная с 9-го или 10-го классов, а также на спецкурсах выездных математических школ. Данный факт установлен в результате опроса учителей математики МБОУ «СОШ № 9» и учащихся, проявляющих повышенный интерес к предмету «математика».
Наиболее востребованными методами решения уравнений высших степеней, которые встречаются при решении олимпиадных, конкурсных задач и в результате подготовки к экзаменам учащимися, являются методы, основанные на применении теоремы Безу, схемы Горнера и введение новой переменной.
Демонстрация результатов исследовательской работы, т.е. способов решения уравнений, не изучаемых в школьной программе по математике, заинтересовала одноклассников.
Заключение
Изучив учебную и научную литературу, Интернет-ресурсы в молодежных образовательных форумах
 Ударение в английском языке
Ударение в английском языке 10 слов с ударением на 1 слог
10 слов с ударением на 1 слог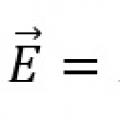 Закон Ома для замкнутой цепи и неоднородного участка цепи
Закон Ома для замкнутой цепи и неоднородного участка цепи