Системы уравнений с параметром. Презентация «Решение линейных уравнений с параметром и модулем Уравнения с параметрами содержащие модуль
21x 2 + 55x + 42 = 0, D = 552 − 4 21 42 = 3025 − 3582 < 0.
Ответ: 1; 2.
§6. Решение уравнений с модулями и параметрами
Рассмотрим несколько уравнений, в которых переменная x стоит под знаком модуля. Напомним, что
x , если x ≥ 0,
x = − x , если x < 0.
Пример 1. Решите уравнение:
а) x − 2 = 3; б) x + 1 − 2x − 3 = 1;
x + 2 |
X =1; г) x 2 − |
6; д) 6x 2 − |
x + 1 |
|||||||||||||||||||||||||||||
x − 1 |
||||||||||||||||||||||||||||||||
а) Если модуль числа равен 3, то это число равно либо 3, либо (− 3 ) , |
||||||||||||||||||||||||||||||||
т. е. x − 2 = 3, x = 5 или x − 2 = − 3, x = − 1. |
||||||||||||||||||||||||||||||||
б) Из определения модуля следует, что |
x + 1 |
X + 1, при x + 1 ≥ 0, |
||||||||||||||||||||||||||||||
т. е. при x ≥ − 1 и |
x + 1 |
= − x − 1 при x < − 1. Выражение |
2x − 3 |
|||||||||||||||||||||||||||||
2 x − 3, если x ≥ 3 |
и равно − 2 x + 3, если x < 3 . |
|||||||||||||||||||||||||||||||
x < −1 |
уравнение |
равносильно |
уравнению |
|||||||||||||||||||||||||||||
− x −1 − |
(− 2 x + 3 ) = 1, из которого следует, что |
x = 5. Но число 5 не |
||||||||||||||||||||||||||||||
удовлетворяет условию x < − 1, следовательно, |
при x < − 1 данное |
|||||||||||||||||||||||||||||||
уравнение решений не имеет. |
||||||||||||||||||||||||||||||||
−1 ≤ x < |
уравнение |
равносильно |
уравнению |
|||||||||||||||||||||||||||||
x + 1− (2x + 3) = 1, из которого следует, что x = 1; |
число 1 удовлетворя- |
|||||||||||||||||||||||||||||||
ет условию − 1 ≤ x < |
||||||||||||||||||||||||||||||||

2010-2011 уч. год., № 5, 8 кл. Математика. Квадратные уравнения
x ≥ |
уравнение |
равносильно |
уравнению |
||||||||||||||||||
x + 1 − (− 2 x − 3 ) = 1, которое имеет решение x = 3. А так как число 3 |
|||||||||||||||||||||
удовлетворяет условию x ≥ |
то оно является решением уравнения. |
||||||||||||||||||||
x + 2 |
|||||||||||||||||||||
в) Если числитель и знаменатель дроби |
имеют одинаковые |
||||||||||||||||||||
x − 1 |
|||||||||||||||||||||
знаки, то дробь положительна, а если разные – то отрицательна, т. е. |
|||||||||||||||||||||
x + 2 |
x + 2 |
Если x ≤ − 2, если x > 1, |
|||||||||||||||||||
x − 1 |
|||||||||||||||||||||
x − 1 |
|||||||||||||||||||||
x + 2 |
Если − 2 < x < 1. |
||||||||||||||||||||
−1 |
|||||||||||||||||||||
При x ≤ − 2 |
ипри x > 1 |
||||||||||||||||||||
исходноеуравнениеравносильноуравнению |
|||||||||||||||||||||
x + 2 |
X =1, x +2 |
X (x −1 ) = x −1, x 2 − x +3 =0. |
|||||||||||||||||||
x − 1 |
|||||||||||||||||||||
Последнее уравнение не имеет решений. |
|||||||||||||||||||||
При − 2 < x < 1 данное уравнение равносильно уравнению |
|||||||||||||||||||||
x + 2 |
X =1, − x −2 + x 2 − x = x −1, x 2 −3 x −1 = 0. |
||||||||||||||||||||
x − 1 |
|||||||||||||||||||||
Найдём корни этого уравнения: |
|||||||||||||||||||||
x = 3 ± 9 + 4 = 3 ± 13 . |
|||||||||||||||||||||
Неравенствам |
− 2 < x < 1 удовлетворяет число 3 − 13 |
Следова- |
|||||||||||||||||||
тельно, это число является решением уравнения. |
|||||||||||||||||||||
x ≥ 0 данное |
уравнение |
равносильно |
уравнению |
||||||||||||||||||
x 2 − x −6 = 0, |
корнями которого являются числа 3 и – 2. Число 3 |
||||||||||||||||||||
удовлетворяет условию x > 0, |
а число – 2 не удовлетворяет этому ус- |
||||||||||||||||||||
ловию, следовательно, только число 3 является решением исходного
x < 0 удовлетворяет число − 3 и не удовлетворяет число 2.
© 2011, ФЗФТШ при МФТИ. Составитель: Яковлева Тамара Харитоновна

2010-2011 уч. год., № 5, 8 кл. Математика. Квадратные уравнения |
||||||||
x ≥ − 1 данное |
уравнение |
равносильно |
уравнению |
|||||
6 x 2 − x − 1 = 0, находим его корни: x = 1 ± |
25 , x = 1 , x |
= −1 . |
||||||
Оба корня удовлетворяют условию x ≥ − 1, |
следовательно, они яв- |
|||||||
ляются решениями данного уравнения. При |
x < − 1 данное уравнение |
|||||||
равносильно уравнению 6 x 2 + x + 1 = 0, которое не имеет решений. |
||||||||
Пусть заданы выражения f (x , a ) и g (x , a ) , |
зависящие от перемен- |
|||||||
ных x |
и a . |
Тогда уравнение |
f (x, a) = g(x, a) |
относительно перемен- |
||||
ной x называется уравнением с параметром a . Решить уравнение с параметром – это значит при любом допустимом значении параметра найти все решения данного уравнения.
Пример 2. Решитеуравнениепривсехдопустимыхзначенияхпараметра a :
а) ax 2 − 3 = 4 a 2 − 2 x 2 ; б) (a − 3 ) x 2 = a 2 − 9;
в) (a − 1 ) x2 + 2 (a + 1 ) x + (a − 2 ) = 0.
x 2 = |
4a 2 + 3 |
Выражение 4 a 2 |
3 > 0 для любого a ; при a > − 2 име- |
|||||
a + 2 |
||||||||
ем два решения: x = |
4a 2 + 3 |
и x = − |
4a 2 |
Если |
a + 2 < 0, то |
|||
a + 2 |
a + 2 |
|||||||
выражение 4 a 2 + 3 < 0, тогда уравнение не имеет решений. a + 2
Ответ: x = ± |
4a 2 + 3 |
При a > − 2; |
при a ≤ − 2 решений нет. |
|
a + 2 |
||||
то x 2 = a + 3. Если a + 3 = 0, |
||||
б) Если a = 3, то x . Если a ≠ 3, |
||||
т.е. если a = − 3, |
то уравнение имеет единственное решение x = 0. Ес- |
|||
ли a < − 3, то уравнение не имеет решений. Если a > − 3 и a ≠ 3, то уравнение имеет два решения: x 1 = a + 3 и x 2 = − a + 3.
© 2011, ФЗФТШ при МФТИ. Составитель: Яковлева Тамара Харитоновна

2010-2011 уч. год., № 5, 8 кл. Математика. Квадратные уравнения |
||||||||||||||||||
a = 1 данное уравнение принимает вид |
4x − 1 = 0, |
|||||||||||||||||
x = 1 |
является его решением. При |
a ≠ 1 данное уравнение является |
||||||||||||||||
квадратным, его дискриминант D 1 равен |
||||||||||||||||||
(a + 1 ) 2 − (a − 1 )(a − 2 ) = 5 a − 1. |
||||||||||||||||||
Если 5 a − 1 < 0, т.е. a < 1 , |
то данное уравнение не имеет решений. |
|||||||||||||||||
Если a = |
то уравнение имеет единственное решение |
|||||||||||||||||
a + 1 |
||||||||||||||||||
x = − |
||||||||||||||||||
a − 1 |
−1 |
|||||||||||||||||
Если a > |
и a ≠ 1, |
то данное уравнение имеет два решения: |
||||||||||||||||
x = − (a + 1 ) ± 5 a − 1 . |
||||||||||||||||||
a − 1 |
−(a +1 ) ± |
|||||||||||||||||
1 при |
a = 1; x = 3 |
при a |
; x = |
5a − 1 |
||||||||||||||
a − 1 |
||||||||||||||||||
при a > 1 |
и a ≠ 1; при a < 1 |
уравнение не имеет решений. |
||||||||||||||||
§7. Решение систем уравнений. Решение задач, сводящихся к квадратным уравнениям
В этом параграфе рассмотрим системы, которые содержат уравнения второй степени.
Пример 1. Решить систему уравнений
2x + 3y = 8,
xy = 2.
В этой системе уравнение 2 x + 3 y = 8 является уравнением первой степени, а уравнение xy = 2 – второй. Решим эту систему методом
© 2011, ФЗФТШ при МФТИ. Составитель: Яковлева Тамара Харитоновна

2010-2011 уч. год., № 5, 8 кл. Математика. Квадратные уравнения
подстановки. Из первого уравнения системы выразим x через y и подставим это выражение для x во второе уравнение системы:
8 − 3y |
4 − |
||||||
y , 4 |
y y = 2. |
||||||
Последнее уравнение сводится к квадратному уравнению
8y − 3y 2 = 4, 3y 2 − 8y + 4 = 0.
Находим его корни: |
|||||||||||||
4 ± 4 |
4 ± 2 |
Y = 2, y |
|||||||||||
Из условия x = 4 − |
получим x = 1, x |
||||||||||||
Ответ: (1;2 ) и |
|||||||||||||
Пример 2. Решите систему уравнений:
x 2 + y 2 = 41,
xy = 20.
Умножим обе части второго уравнения на 2 и сложим с первым
уравнением системы: |
x 2 + y 2 + 2xy = 41 + 20 2, |
(x + y ) 2 = 81, откуда |
||||
следует, что x + y = 9 или x + y = − 9. |
||||||
Если x + y = 9, то |
x = 9 − y . Подставим это выражение для x во |
|||||
второе уравнение системы: |
||||||
(9 − y ) y = 20, y 2 − 9 y + 20 = 0, |
||||||
y = 9 ± 81 − 80 = 9 ± 1 , y = 5, y |
4, x = 4, x = 5. |
|||||
Из условия x + y = − 9 получим решения (− 4; − 5) и (− 5; − 4 ) . |
||||||
Ответ: (± 4;± 5) , (± 5;± 4) . |
||||||
Пример 3. Решите систему уравнений: |
||||||
y = 1, |
||||||
x − |
||||||
x − y |
||||||
Запишем второе уравнение системы в виде
( x − y )( x + y ) = 5.
© 2011, ФЗФТШ при МФТИ. Составитель: Яковлева Тамара Харитоновна

2010-2011 уч. год., № 5, 8 кл. Математика. Квадратные уравнения
Используя уравнение x − y = 1, получаем: x + y = 5. Таким образом, получаем систему уравнений, равносильную дан-
x − |
y = 1, |
|
y = 5. |
||
Сложим эти уравнения, получим: 2 x = 6, |
x = 3, x = 9. |
||||||
Подставляя значение x = 9 в первое уравнение |
системы, получа- |
||||||
ем 3 − y = 1, откуда следует, что y = 4. |
|||||||
Ответ: (9;4 ) . |
(x + y)(x |
Y −4 ) = −4, |
|||||
Пример 4. Решите систему уравнений: (x 2 + y 2 ) xy = − 160. |
|||||||
xy = v; |
|||||||
Введём новые переменные |
x + y = u |
||||||
x2 + y2 = x2 + y2 + 2 xy − 2 xy = (x + y) 2 − 2 xy = u2 − 2 v, |
|||||||
u (u −4 ) = −4, |
|||||||
система приводится к виду (u 2 − 2 v ) v = − 160. |
|||||||
Решаем уравнение: |
|||||||
u (u − 4) = − 4, u 2 − 4u + 4 = 0, (u − 2) 2 = 0, u = 2. |
|||||||
Подставляем это значение для u в уравнение: |
|||||||
(u 2 − 2v ) v = − 160, (4 − 2v ) v = − 160, 2v 2 − 4v − 160 = 0, |
|||||||
v 2 − 2v − 80 = 0, v = 1± 1 + 80 = 1± 9, v = 10, v |
= −8. |
||||||
Решаем две системы уравнений: |
|||||||
x + y = 2, |
|||||||
x + y = 2, |
|||||||
и |
|||||||
xy = 10 |
xy = − 8. |
||||||
Обесистемырешаемметодомподстановки. Дляпервойсистемыимеем: |
|||||||
x = 2 − y , (2 − y ) y = 10, y 2 − 2 y + 10 = 0. |
|||||||
Полученное квадратное уравнение не имеет решений. Для второй системы имеем: x = 2 − y , (2 − y ) y = − 8, y 2 − 2 y − 8 = 0.
y = 1 ± 1 + 8 = 1 ± 3, y 1 = 4, y 2 = − 2. Тогда x 1 = − 2 и x 2 = 4. Ответ: (− 2;4 ) и (4; − 2 ) .
© 2011, ФЗФТШ при МФТИ. Составитель: Яковлева Тамара Харитоновна

умноженное на 3, получим:
2010-2011 уч. год., № 5, 8 кл. Математика. Квадратные уравнения
Пример 5. Решите систему уравнений:
x2 + 4 xy = 3,
y2 + 3 xy = 2.
Из первого уравнения умноженного на 2, вычтем второе уравнение,
2 x2 − xy − 3 y2 = 0.
Если y = 0, тогда и x = 0, но пара чисел (0;0 ) не является решением исходной системы. Разделим в полученном уравнении обе части ра-
венства на y 2 , |
||||||||||||||||||||||||
1 ± 5 , x = 2 y и x = − y. |
||||||||||||||||||||||||
−3 |
= 0, |
|||||||||||||||||||||||
y |
||||||||||||||||||||||||
Подставляем |
значение |
x = |
3y |
первое уравнение |
||||||||||||||||||||
9 y 2 + 6 y 2 = 3, 11y 2 = 4, y = |
, x = |
, x = − |
||||||||||||||||||||||
Подставляем значение x = − y в первое уравнение системы: y 2 − 4 y 2 = 3, − 3 y 2 = 3.
Решений нет.
Пример 9. Найтивсезначенияпараметра a , прикоторыхсистемауравнений
x2 + (y − 2 ) 2 = 1,
y = ax2 .
имеет хотя бы одно решение.
Данная система называется системой с параметром. Их можно решить аналитическим методом, т.е. с помощью формул, а можно применить так называемый графический метод.
Заметим, что первое уравнение задаёт окружность с центром в точке (0;2 ) с радиусом 1. Второе уравнение при a ≠ 0 задаёт параболу с вершиной в начале координат.
Если a 2
Вслучаеа) параболакасаетсяокружности. Извторогоуравнениясистемыследу-
ет, что x 2 = y / a , |
подставляем это значения для |
x2 |
в первоеуравнение: |
||||||||||
1 |
|||||||||||||
+(y −2 ) |
= 1, |
+ y |
− 4 y + 4 = 1, y |
4 − a y + 3 |
= 0. |
||||||||
В случае касания в силу симметрии существует единственное значение y , поэтому дискриминант полученного уравнения должен быть
равен 0. Так как ордината y точки касания положительная и т.к.
y = 2 |
− a |
получаем, |
|||||||||||||||
> 0; D |
1 2 |
||||||||||||||||
4 − a |
4 − a |
− 12 = 0, |
4 − a |
> 0 |
|||||||||||||
получаем: 4 |
= 2 |
= 4 −2 |
|||||||||||||||
a = |
4 + 2 3 |
4 + 2 3 |
2 + |
||||||||||||||
(4 − 2 3)(4 + 2 3) = |
16 − 12 = |
||||||||||||||||
4 − 2 3 |
|||||||||||||||||
Если a > 2 + 2 3 , то парабола будет пересекать окружность в 4 точ-
© 2011, ФЗФТШ при МФТИ. Составитель: Яковлева Тамара Харитоновна

2010-2011 уч. год., № 5, 8 кл. Математика. Квадратные уравнения
Следовательно, система имеет хотя бы одно решение, если
a ≥ 2 + 2 3 .
Пример 10. Сумма квадратов цифр некоторого натурального двузначного числа на 9 больше удвоенного произведения этих цифр. После деления этого двузначного числа на сумму его цифр в частном получается 4 и в остатке 3. Найти это двузначное число.
Пусть двузначное число равно 10 a + b , где a и b – цифры этого числа. Тогда из первого условия задачи получаем: a 2 + b 2 = 9 + 2 ab , а из второго условия получаем: 10 a + b = 4 (a + b ) + 3.
a2 + b2 = 9 + 2 ab,
Решаем систему уравнений: 6 a − 3 b = 3.
Из второго уравнения системы получаем
6a − 3b = 3, 2a − b = 1, b = 2a − 1.
Подставляемэтозначениедля b впервоеуравнениесистемы:
a 2 + (2a − 1) 2 = 9 + 2a (2a − 1) , 5a 2 − 4a + 1 = 9 + 4a 2 − 2a ,
a 2 − 2a − 8 = 0, D 1 = 1 + 8 = 9, a = 1 ± 3, a 1 = 4, a 2 = − 2 < 0, b 1 = 7.
Ответ: 47.
Пример 11. После смешения двух растворов, один из которых содержал 48 г, а другой 20 г, безводного йодистого калия, получили 200 г нового раствора. Найдите концентрацию каждого из первоначальных растворов, если концентрация первого раствора была на 15% больше концентрации второго.
Обозначим через x % – концентрацию второго раствора, а через (x + 15 ) % – концентрацию первого раствора.
(x + 15 )% |
x % |
|||
I раствор |
II раствор |
|||
В первом растворе 48 г составляет (x + 15 ) % от веса всего раствора,
поэтому вес раствора равен x 48 + 15 100. Во втором растворе 20 г со-
© 2011, ФЗФТШ при МФТИ. Составитель: Яковлева Тамара Харитоновна
«Линейное уравнение с двумя переменными» - Равенство, содержащее две переменные, называется уравнением с двумя переменными. -Что называется уравнением с двумя переменными? Приведите примеры. -Какое уравнение с двумя переменными называется линейным? Линейное уравнение с двумя переменными. Определение: Алгоритм доказательства, что данная пара чисел является решением уравнения:
«Решение показательных уравнений» - Сведение к одному основанию. Вынесение за скобки. Т. Виета. Графический способ. Показательным уравнением называют уравнение, содержащее переменную в показателе степени. Решение показательных уравнений. Устная работа. ab+ac=a(b+c). Степени. 2.Решить уравнение: Свойство. Виды и способы решения показательных уравнений.
«Графический способ решения уравнений» - Ответ: один корень, х=-1. Два корня. Решить графически уравнение (х+1)/(х-2)=2. Построить график функции y=x?+6x+8. Практикум по решению уравнений графическим способом Подготовка к зачету. Построить графики функций. Построить график функции y=(x+1)/(x-2). 1. Перенесем 8 в правую часть уравнения. Корней нет.
«Решение целых уравнений» - «Уравнения, в которых скопом Корни, степень, неравенств бездна. Три великих математика. Удачи в дальнейшем изучении методов решения уравнений. Осевая симметрия присуща большинству видов растений и животных. Центральная. В животном мире 2 вида симметрии. Диктант. Осевая. Определите методы решения уравнений.
«Уравнения с логарифмами» - Логарифмические уравнения. Реши устно уравнения. Формулы преобразования логарифмов. Уравнение. Определение. Таблицы логарифмов. Определение логарифма. Определение и свойства логарифма. Логарифмическая линейка. Функция. Наушники или колонки. Область определения. Подходы к решению. Решить уравнение. Гимназия.
«Иррациональные уравнения» - На контроль д/з выполнили: №419 (в,г) Сафиуллина, №418(в,г) Кульмухаметов, №420(в,г)Шагеев. 2 урок Решение систем уравнений. Урок 1 Тема: Решение иррациональных уравнений. 1.Какие из следующих уравнений являются иррациональными: Цели: Познакомить учащихся с решениями некоторых видов иррациональных уравнений.
Всего в теме 49 презентаций
Уравнения с параметрами

Математика – единственный совершенный метод, позволяющий провести самого себя за нос. Альберт Эйнштейн

№ 1 Найдите все значения a, при каждом из которых уравнение x² + (a + 5)² = |x + a + 5| + |x – a -5| имеет ровно три корня.
РЕШЕНИЕ Уравнение не изменится, если заменить x числом –x . Следовательно, уравнение имеет чётное число ненулевых решений. Значит, три решения уравнения имеет только тогда, когда одно из них 0. Поставим x = 0 .
Получим: (a + 5)² = 2|a + 5|
Откуда a + 5 = 0 или |a + 5| = 2.

Если a + 5 = 0, уравнение принимает вид x² = 2|x| и имеет ровно три решения: -2, 0, 2. Из a + 5 = 0 получаем: a = -5. Если |a +5| = 2, уравнение принимает вид x² + 4 = |x + 2| + |x – 2|.
 2 уравнение принимает вид x² - 2x + 4 = 0 и не имеет решений. Аналогично решений нет при x Ответ: a = -5. " width="640"
2 уравнение принимает вид x² - 2x + 4 = 0 и не имеет решений. Аналогично решений нет при x Ответ: a = -5. " width="640"
При -2 ≤ x ≤ 2 уравнение имеет единственное решение 0. При x 2 уравнение принимает вид x² - 2x + 4 = 0 и не имеет решений. Аналогично решений нет при x Ответ: a = -5.

№ 2
Найдите все значения параметра a, при котором уравнение f(x) = |2a + 5|x
имеет 6 решений, где f -- чётная периодическая функция, с периодом Т = 2, определённая на всей числовой прямой, причём f(x) = ax², если 0≤x≤1 .
РЕШЕНИЕ Если а = 0, функция f(x) тождественно равна нулю, и её график имеет с прямой y = 5x единственную общую точку.
 0, то 9а = -25. Положительных решений нет. Следовательно, случай а 0 невозможен. " width="640"
0, то 9а = -25. Положительных решений нет. Следовательно, случай а 0 невозможен. " width="640"
Пусть а = 0, (рис. 1). Решение х = 0 есть при всех а. Нужно ещё ровно пять решений. Единственный возможный случай показан на рисунке: прямая проходит через точку (5 ; а). Составим уравнение |2a + 5| ∙ 5 = a. Так как а 0, то 9а = -25. Положительных решений нет. Следовательно, случай а 0 невозможен.


№ 3 Найдите все значения а, при каждом из которых функция f(x) = x² - 3|x - a²| - 5x имеет более двух точек экстремума. РЕШЕНИЕ При х ≥ а² f (x) = x² - 8x + 3a², поэтому график функции есть часть параболы с ветвями, направленными вверх, и осью симметрии х = 4.



Обе параболы проходят через точку (а² ; f(a²)). Функция y = f(x) имеет более двух точек экстремума, а именно три, в единственном случае (рис. 1): 1
Ответ: -2

СПАСИБО ЗА ВНИМАНИЕ!
К задачам с параметром можно отнести, например, поиск решения линейных и квадратных уравнений в общем виде, исследование уравнения на количество имеющихся корней в зависимости от значения параметра.
Не приводя подробных определений, в качестве примеров рассмотрим следующие уравнения:
у = kx, где x, y – переменные, k – параметр;
у = kx + b, где x, y – переменные, k и b – параметр;
аx 2 + bх + с = 0, где x – переменные, а, b и с – параметр.
Решить уравнение (неравенство, систему) с параметром это значит, как правило, решить бесконечное множество уравнений (неравенств, систем).
Задачи с параметром можно условно разделить на два типа:
а) в условии сказано: решить уравнение (неравенство, систему) – это значит, для всех значений параметра найти все решения. Если хотя бы один случай остался неисследованным, признать такое решение удовлетворительным нельзя.
б) требуется указать возможные значения параметра, при которых уравнение (неравенство, система) обладает определенными свойствами. Например, имеет одно решение, не имеет решений, имеет решения, принадлежащие промежутку и т. д. В таких заданиях необходимо четко указать, при каком значении параметра требуемое условие выполняется.
Параметр, являясь неизвестным фиксированным числом, имеет как бы особую двойственность. В первую очередь, необходимо учитывать, что предполагаемая известность говорит о том, что параметр необходимо воспринимать как число. Во вторую очередь, свобода обращения с параметром ограничивается его неизвестностью. Так, например, операции деления на выражение, в котором присутствует параметр или извлечения корня четной степени из подобного выражения требуют предварительных исследований. Поэтому необходима аккуратность в обращении с параметром.
Например, чтобы сравнить два числа -6а и 3а, необходимо рассмотреть три случая:
1) -6a будет больше 3a, если а отрицательное число;
2) -6а = 3а в случае, когда а = 0;
3) -6а будет меньше, чем 3а, если а – число положительное 0.
Решение и будет являться ответом.
Пусть дано уравнение kx = b. Это уравнение – краткая запись бесконечного множества уравнений с одной переменной.
При решении таких уравнений могут быть случаи:
1. Пусть k – любое действительное число не равное нулю и b – любое число изR, тогда x = b/k.
2. Пусть k = 0 и b ≠ 0, исходное уравнение примет вид 0 · x = b. Очевидно, что у такого уравнения решений нет.
3. Пусть k и b числа, равные нулю, тогда имеем равенство 0 · x = 0. Его решение – любое действительное число.
Алгоритм решения такого типа уравнений:
1. Определить «контрольные» значения параметра.
2. Решить исходное уравнение относительно х при тех значениях параметра, которые были определены в первом пункте.
3. Решить исходное уравнение относительно х при значениях параметра, отличающихся от выбранных в первом пункте.
4. Записать ответ можно в следующем виде:
1) при … (значения параметра), уравнение имеет корни …;
2) при … (значения параметра), в уравнении корней нет.
Пример 1.
Решить уравнение с параметром |6 – x| = a.
Решение.
Легко видеть, что здесь a ≥ 0.
По правилу модуля 6 – x = ±a, выразим х:
Ответ: х = 6 ± a, где a ≥ 0.
Пример 2.
Решить уравнение a(х – 1) + 2(х – 1) = 0 относительно переменной х.
Решение.
Раскроем скобки: aх – а + 2х – 2 = 0
Запишем уравнение в стандартном виде: х(а + 2) = а + 2.
В случае, если выражение а + 2 не нуль, т. е. если а ≠ -2, имеем решение х = (а + 2) / (а + 2), т.е. х = 1.
В случае, если а + 2 равно нулю, т.е. а = -2, то имеем верное равенство 0 · x = 0, поэтому х – любое действительное число.
Ответ: х = 1 при а ≠ -2 и х € R при а = -2.
Пример 3.
Решить уравнение x/a + 1 = а + х относительно переменной х.
Решение.
Если а = 0, то преобразуем уравнение к виду а + х = а 2 + ах или (а – 1)х = -а(а – 1). Последнее уравнение при а = 1 имеет вид 0 · x = 0, следовательно, х – любое число.
Если а ≠ 1, то последнее уравнение примет вид х = -а.
Данное решение можно проиллюстрировать на координатной прямой (рис. 1)
Ответ: нет решений при а = 0; х – любое число при а = 1; х = -а при а ≠ 0 и а ≠ 1.
Графический метод
Рассмотрим еще один способ решения уравнений с параметром – графический. Этот метод применяется достаточно часто.
Пример 4.
Сколько корней в зависимости от параметра a имеет уравнение ||x| – 2| = a?
Решение.
Для решения графическим методом строим графики функций y = ||x| – 2| и y = a (рис. 2) .
На чертеже наглядно видны возможные случаи расположения прямой y = a и количество корней в каждом из них.
Ответ: корней у уравнения не будет, если а < 0; два корня будет в случае, если a > 2 и а = 0; три корня уравнение будет иметь в случае а = 2; четыре корня – при 0 < a < 2.

Пример 5.
При каком а уравнение 2|x| + |x – 1| = a имеет единственный корень?
Решение.
Изобразим графики функций y = 2|x| + |x – 1| и y = a. Для y = 2|x| + |x – 1|, раскрыв модули методом промежутков, получим:
{-3x + 1, при x < 0,
y = {x + 1, при 0 ≤ x ≤ 1,
{3x – 1, при x > 1.
На рисунке 3 хорошо видно, что единственный корень уравнение будет иметь только при а = 1.
Ответ: а = 1.
Пример 6.
Определить число решений уравнения |x + 1| + |x + 2| = a в зависимости от параметра а?
Решение.
График функции y = |x + 1| + |x + 2| будет представлять собой ломаную. Ее вершины будут располагаться в точках (-2; 1) и (-1; 1) (рисунок 4)
.
Ответ: если параметр a будет меньше единицы, то корней у уравнения не будет; если а = 1, то решение уравнения является бесконечное множество чисел из отрезка [-2; -1]; если значения параметра а будут больше одного, то уравнение будет иметь два корня.
Остались вопросы? Не знаете, как решать уравнения с параметром?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
 Чиновники-академики уволены с госслужбы
Чиновники-академики уволены с госслужбы Учебная книга по химии Вода, неэлектролиты и электролиты
Учебная книга по химии Вода, неэлектролиты и электролиты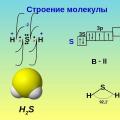 Соли сероводородной кислоты (сульфиды), их растворимость в воде и взаимодействие с минеральными кислотами
Соли сероводородной кислоты (сульфиды), их растворимость в воде и взаимодействие с минеральными кислотами