Определение числовой последовательности способы задания примеры. Числовые последовательности и способы их задания. Геометрическое изображение числовых последовательностей. Примеры неограниченно возрастающих последовательностей
ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ VI
§ 127. Числовые последовательности и способы их задания. Конечныеи бесконечные последовательности.
Рассмотрим следующие три совокупности чисел:
Естественно считать, что каждое число в любой из этих совокупностей снабжено номером в соответствии с тем местом, которое оно занимает в этой совокупности. Например, во второй совокупности число 1 имеет номер 1, число - 1 / 2 номер 2, число 1 / 3 номер 3 и т. д.
Наоборот, какой бы номер мы ни указали, в каждой из этих совокупностей найдется число, снабженное этим номером. Например, номер 2 в первой последовательности имеет число 2, во второй - число - 1 / 2 , в третьей - число sin 2. Аналогично номер 10 имеют: в первой последовательности - число 10, во второй - число - 1 / 10 , в третьей - число sin 10 и т. д. Таким образом, в приведенных выше совокупностях каждое число имеет вполне определенный номер и полностью определяется этим номером.
Совокупность чисел, каждое из которых снабжено своим номером п (п = 1, 2, 3, ...), называется числовой последовательностью.
Отдельные числа последовательности называются ее членами и обозначаются обычно так: первый член a 1 , второй a 2 , .... п -й член a n и т. д. Вся числовая последовательность обозначается
a 1 , a 2 , a 3 , ... , a n , ... или {a n }.
Задать числовую последовательность - это знанит указать, как отыскивается тот или иной ее член, если известен номер занимаемого им места. Существует много различных способов задания числовых последовательностей. Ниже мы остановимся на некоторых из них.
1. Обычно числовая последовательность задается с помощью формулы, позволяющей по номеру члена последовательности определить этот член. Например, если известно, что при любом п
a n = n 2 ,
a 1 = 1, a 2 = 4, a 3 = 9
и т. д. При a n = sin π / 2 п мы получим: a 1 = sin π / 2 = 1, a 2 = sin π = 0, a 3 = sin 3 π / 2 = - 1, a 4 = sin 2π = 0 и т. д.
Формула, позволяющая найти любой член числовой последовательности по его номеру, называется формулой общего члена числовой последовательности.
2. Бывают случаи, когда последовательность задается посредством описания ее членов. Например, говорят, что последовательность
1,4; 1,41; 1,414; 1,4142; ...
составлена из приближенных значений √2 с недостатком с точностью до 0,1; 0,01; 0,001; 0,0001 и т. д. В подобных случаях иногда вообще нельзя установить формулу общего члена; тем не менее последовательность оказывается полностью определенной.
3. Иногда указывается несколько первых членов последовательности, а все остальные члены определяются этими заданными членами по тому или иному правилу. Пусть, например,
a 1 = 1, a 2 = 1,
а каждый последующий член определяется как сумма двух предыдущих. Другими словами, при любом п > 3
a n = a n - 1 + a n - 2
Так определяется числовая последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34, .... члены которой носят название «чисел Фибоначчи» [по имени итальянского математика Леонарда Пизанского (около 1170-1250), которого называли также Фибоначчи, что означает «сын Боначчо»].Они обладают многими интересными свойствами, рассмотрение которых, однако, выходит за пределы нашей программы.
Последовательность может содержать как конечное, так и бесконечное число членов.
Последовательность, состоящая из конечного числа членов, называется конечной, а последовательность, состоящая из бесконечного числа членов, - бесконечной последовательностью.
Например, последовательность всех четных положительных чисел 2, 4, 6, 8, 10, 12, ... бесконечна, а последовательность однозначных четных положительных чисел 2, 4, 6, 8 конечна.
Упражнения
932. Написать 4 первых числа последовательности с общим членом:

933. Найти формулу общего члена для каждой из данных последовательностей:
а) 1, 3, 5, 7, 9, ... ; . д) tg 45°, tg 22°30", tg 11°15", ... ;
б) 2, 4, 6, 8, 10, ... ; е) 1, - 1 / 2 , 1 / 4 , - 1 / 8 , 1 / 16 , ... ;
в) 3, -3, 3, -3, 3, ... ; ж) 1, 9, 25, 49, 81.....
г) 1 / 3 , 1 / 9 , 1 / 27 , 1 / 81 , ....;
934. Является ли конечной последовательность всех положительных корней уравнения:
а) sin х = х - 1; б) tg х = х ; в) sin х = ах + b ?
Обучающая цель : дать понятие и определение числовой последовательности, рассмотреть способы задания числовых последовательностей, решать упражнения.
Развивающая цель : развивать логическое мышление, познавательные навыки, техники вычисления, навыки сравнения при выборе формул, навыки учебного труда
Воспитательная цель : воспитание положительных мотивов к учебе, добросовестного отношения к труду, дисциплинированности.
Тип урока : урок закрепления метериала.
Оборудование : интерактивная доска, тестирующее установка ACTIVwote,ACTIVwand,ACTIVslate, раздаточный материал.
План урока
- Организация урока.
- Повторение теоретического материала. Фронтальный опрос. Историческая справка.
- Закрепление: Решение упражнений по теме «Способы задания числовых последовательностей».
- Проверка знаний. Тест
- Домашнее задание.
Ход урока
II . Повторение теоретического материала.
1) Фронтальныйопрос.
1. Что называется числовой последовательностью?
Ответ : Множество чисел, элементы которого можно пронумеровать.
2. Приведи пример числовой последовательности.
Ответ :
2,4,6,8,10,…..
1,3,5,7,9,11,…..
3,6,9,12,15,….
3. Что называется членами числовой последовательности?
Ответ : Числа, составляющие числовую последовательность.
а 1 =2,а 2 =4,а 3 =6,а 4 =8,….
а 1 =1,а 2 =3,а 3 =5,а 4 =7,….
а 1 =3,а 2 =6,а 3 =9,а 4 =12,….
4. Что такое общий член числовой последовательности?
Ответ : ап называется общим членом последовательности,а саму последовательность коротко обозначают через {ап}.
5. Как обозначают числовую последовательность?
Ответ : Обычно числовую последовательность обозначают малыми буквами латинского алфавита с индексами, указывающими на номер этого члена в последовательности: а 1 ,а 2 ,а 3 ,а 4 ,….,а п,…
5. Когда числовую последовательность считаются заданной?
Ответ : Если мы можем указать любой член последовательности.
2) Историческая справка.
По словам математика Лейбница «кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет».

ФИБОНАЧЧИ (Леонардо из Пизы)
Fibonacci (Leonardo of Pisa), ок . 1175–1250
Итальянский математик. Родился в Пизе, стал первым великим математиком Европы позднего Средневековья. В математику его привела практическая потребности установить деловые контакты. Он издавал свои книги по арифметике, алгебре и другим математическим дисциплинам. От мусульманских математиков он узнал о системе цифр, придуманной в Индии и уже принятой в арабском мире, и уверился в ее превосходстве (эти цифры были предшественниками современных арабских цифр).
Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Будучи рожденным в Пизе в богатой купеческой семье, он пришел в математику благодаря сугубо практической потребности установить деловые контакты. В молодости Леонардо много путешествовал, сопровождая отца в деловых поездках. Например, мы знаем о его длительном пребывании в Византии и на Сицилии. Во время таких поездок он много общался с местными учеными.
Числовой ряд, носящий сегодня его имя, вырос из проблемы с кроликами, которую Фибоначчи изложил в своей книге «Liber abacci», написанной в 1202 году:
Человек посадил пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару?
Можете убедиться, что число пар в каждый из двенадцати последующих месяцев месяцев будет соответственно 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
Иными словами, число пар кроликов создает ряд, каждый член в котором - сумма двух предыдущих. Он известен как ряд Фибоначчи , а сами числа - числа Фибоначчи . Оказывается, эта последовательность имеет множество интересных с точки зрения математики свойств. Вот пример: вы можете разделить линию на два сегмента, так что соотношение между большим и меньшим сегментом будет пропорционально соотношению между всей линией и большим сегментом. Этот коэффициент пропорциональности, приблизительно равный 1,618, известен как золотое сечение . В эпоху Возрождения считалось, что именно эта пропорция, соблюденная в архитектурных сооружениях, больше всего радует глаз. Если вы возьмете последовательные пары из ряда Фибоначчи и будете делить большее число из каждой пары на меньшее, ваш результат будет постепенно приближаться к золотому сечению.
С тех пор как Фибоначчи открыл свою последовательность, были найдены даже явления природы, в которых эта последовательность, похоже, играет немаловажную роль. Одно из них - филлотаксис (листорасположение) - правило, по которому располагаются, например, семечки в соцветии подсолнуха.Семечки у подсолнуха упорядочены в две спирали. Числа, обозначающие количество семечек в каждой из спиралей, являются членами удивительной математической последовательности.
Семечки упорядочены в два ряда спиралей, один из которых идет по часовой стрелке, другой против. И каково же число семян в каждом случае? 34 и 55.
Числа Фибоначчи 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
Последовательность чисел, каждый член которой равен сумме двух предыдущих, имеет множество любопытных свойств.
III. Закрепление.
Работа по учебнику (цепочкой)
№343 Напишите первые пять членов последовательности.
1. а n =2 n +1/2 n
2. х n =3n2+2 n+1
3.
1. Решение:
а n =2 n +1/2 n
![]()
![]()
![]()
![]()
![]()
Ответ
:![]()
2. Решение:
n=1, x 1 =3*1 2 +2*1+1=3+2+1=6
n=2, x 2 =3*2 2 +2*2+1=3*4+4+1=12+5=17
n=3, x 3 =3*3 2 +2*3+1=27+6+1=34
n=4, x 4 =3*4 2 +2-4+1=3*16+8+1=48+9=57
n=5, x 5 =3*5 2 +2*5+1=3*25+10+1=75+11=86
Ответ : 6,17,34,57,86…….
3. Решение:
![]()
![]()
![]()
![]()
![]()
Ответ
: 
№344. Напишите формулу общего члена последовательности натуральных чисел, кратных 3.
Ответ : 0,3,6,9,12,15,.... 3n, а n =3n
№345. Напишите формулу общего члена последовательности натуральных чисел, кратных 7.
Ответ : 0,7,14,25,28,35,42.... 7n, а n =7n
№346 Напишите формулу общего члена последовательности натуральных чисел,которые при делении на 4 дают в остатке 1.
Ответ :5,9,13,17,21....... 4 n +1 , а n =4n+1
№347 Напишите формулу общего члена последовательности натуральных чисел,которые при делении на 5 дают в остатке 2.
Ответ : а n =5n+2, 7.12,17,22, 27,.... 5 n +2
№348 Напишите формулу общего члена последовательности.
Алгебра. 9 класс
Урок № 32
Дата:_____________
Учитель: Горбенко Алена Сергеевна
Тема: Числовая последовательность, способы ее задания и свойства
Тип урока: комбинированный
Цель урока: дать понятие и определение числовой последовательности, рассмотреть способы
задания числовых последовательностей
Задачи:
Образовательные: ознакомить учащихся с понятием числовой последовательности и членом
числовой последовательности; ознакомиться с аналитическим, словесным, рекуррентным и
графическим способами задания числовой последовательности; рассмотреть виды числовой
последовательности; подготовка к ВОУД;
Развивающие: развитие математической грамотности, мышления, техники вычисления, навыки
сравнения при выборе формулы; привитие интереса к математике;
Воспитательные: воспитание навыков самостоятельной деятельности; четкость и
организованность в работе; дать каждому ученику достичь успеха;
Оборудование: Школьные принадлежности, доска, мел, учебник, раздаточный материал.
Ход урока
I. Организационный момент
Взаимное приветствие;
Фиксация отсутствующих;
Объявление темы урока;
Постановка целей и задач урока учащимися.
Последовательность одно из самых основных понятий математики. Последовательность может
быть составлена из чисел, точек, функций, векторов и т.д.
Сегодня на уроке мы познакомимся с понятием " числовая последовательность", узнаем, какие
могут быть последовательности, познакомимся со знаменитыми последовательностями.

II. Актуализация опорных знаний.
Вам известны функции, определённые на всей числовой прямой или на её непрерывных
III.
промежутках:
линейная функция у = кх+в,
квадратичная функция у = ах2+вх+с,
функция у =
функция у =|х|.
Подготовка к восприятию новых знаний
прямая пропорциональность у = кх,
обратная пропорциональность у =к/х,
кубическая функция у = х3,
,
Но бывают функции, заданные на других множествах.
Пример. Во многих семьях есть обычай, своего рода ритуал: в день рождения ребёнка
родители подводят его к дверному косяку и торжественно отмечают на нём рост именинника.
Ребёнок растёт, и на косяке с годами возникает целая лесенка отметок. Три, пять, два: Такова
последовательность приростов от года к году. Но есть и другая последовательность, и именно
её члены аккуратно выписывают рядом с засечками. Это последовательность значений роста.
Две последовательности связаны друг с другом.
Вторая получается из первой сложением.
Рост это сумма приростов за все предыдущие годы.
Рассмотреть ещё несколько задач.
Задача 1. На складе имеется 500 т угля, каждый день подвозят по 30 т. Сколько угля будет
на складе в 1 день? 2 день? 3 день? 4 день? 5 день?
(Ответы учащихся записываются на доске: 500, 530, 560, 590, 620).
Задача 2. В период интенсивного роста человек растёт в среднем на 5 см в год. Сейчас рост
у ученика С. 180 см. Какого роста он будет в 2026 году? (2м 30 см). Но этого быть не
может. Почему?
Задача 3. Ежедневно каждый болеющий гриппом человек может заразить 4 окружающих.
Через сколько дней заболеют все ученики нашей школы (300 человек)? (Через 4 дня).
Это примеры функций, заданных на множестве натуральных чисел – числовые
последовательности.
Ставится цель урока: Найти способы нахождения любого члена последовательности.
Задачи урока: Выяснить, что такое числовая последовательность и как задаются
последовательности.
IV. Изучение нового материала
Определение: Числовая последовательность – это функция, заданная на множестве
натуральных чисел (последовательности составляют такие элементы природы, которые
можно пронумеровать).
Понятие числовой последовательности возникло и развилось задолго до создания учения о
функции. Вот примеры бесконечных числовых последовательностей, известных еще в
древности:
1, 2, 3, 4, 5, : последовательность натуральных чисел;
2, 4, 6, 8, 10, : последовательность четных чисел;
1, 3, 5, 7, 9, : последовательность нечетных чисел;
1, 4, 9, 16, 25, : последовательность квадратов натуральных чисел;
2, 3, 5, 7, 11, : последовательность простых чисел;
,
1,
Число членов каждого из этих рядов бесконечно; первые пять последовательностей
, : последовательность чисел, обратных натуральным.
,
монотонно возрастающие, последняя монотонно убывающая.

Обозначение: у1, у2, у3, у4, у5,:
1, 2, 3, 4, 5, :п,:порядковый номер члена последовательности.
(уп) последовательность, уп пый член последовательности.
(ап) последовательность, ап пый член последовательности.
ап1 предыдущий член последовательности,
ап+1 последующий член последовательности.
Последовательности бывают конечными и бесконечными, возрастающие и убывающие.
Задания учащимся: Записать первые 5 членов последовательности:
От первого натурального числа увеличение на 3.
От 10 увеличение в 2 раза и уменьшение на 1.
От числа 6 чередовать увеличение на 2 и увеличение в 2 раза.
Эти числовые ряды тоже называются числовыми последовательностями.
Способы задания последовательностей:
Словесный способ.
Правила задания последовательности описываются словами, без указания формул или
когда закономерности между элементами последовательности нет.
Пример 1.Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, .... .
Пример 2. Произвольный набор чисел: 1, 4, 12, 25, 26, 33, 39, ... .
Пример 3. Последовательность чётных чисел 2, 4, 6, 8, 10, 12, 14, 16, ...
Аналитический способ.
Любой nй элемент последовательности можно определить с помощью формулы.
Пример 1. Последовательность чётных чисел: y = 2n.
Пример 2.Последовательность квадрата натуральных чисел: y = n2;
1, 4, 9, 16, 25, ..., n2, ... .
Пример 3. Стационарная последовательность: y = C; C, C, C, ...,C, ...
Частный случай: y = 5; 5, 5, 5, ..., 5, ... .
Пример 4. Последовательность y = 2n;
2, 22, 23, 24, ..., 2n, ... .
Рекуррентный способ.
Указывается правило, позволяющее вычислить nй элемент последовательности, если
известны её предыдущие элементы.
Пример 1. Арифметическая прогрессия: a1=a, an+1=an+d, где a и d – заданные числа, d
разность арифметической прогрессии. Пусть a1=5, d=0,7, тогда арифметическая прогрессия
будет иметь вид: 5; 5,7; 6,4; 7,1; 7,8; 8,5; ... .
Пример 2. Геометрическая прогрессия: b1= b, bn+1= bnq, где b и q – заданные числа, b
0,
0; q – знаменатель геометрической прогрессии. Пусть b1=23, q=½, тогда геометрическая
q
прогрессия будет иметь вид: 23; 11,5; 5,75; 2,875; ... .
4) Графический способ. Числовая последовательность
задается графиком, который представляет собой
изолированные точки. Абсциссы этих точек - натуральные
числа: n=1; 2; 3; 4; ... . Ординаты - значения членов
последовательности: a1; a2; a3; a4;…
Пример: Запишите все пять членов числовой последовательности,
заданной графическим способом.
Решение.
Каждая точки в этой координатной плоскости имеет
координаты (n; an). Выпишем координаты отмеченных точек
по возрастанию абсциссы n.
Получаем: (1; 3), (2; 1), (3; 4), (4; 6), (5; 7).
Следовательно, a1= 3; a2=1; a3=4; a4=6; a5 =7.

Ответ: 3; 1; 4; 6; 7.
V. Первичное закрепление изученного материала
Пример 1. Составить возможную формулу nго элемента последовательности (yn):
а) 1, 3, 5, 7, 9, 11, ...;
б) 4, 8, 12, 16, 20, ...;
Решение.
а) Это последовательность нечётных чисел. Аналитически эту последовательность можно
задать формулой y = 2n+1.
б) Это числовая последовательность, у которой последующий элемент больше предыдущего
на 4. Аналитически эту последовательность можно задать формулой y = 4n.
Пример 2. Выписать первые десять элементов последовательности, заданной рекуррентно: y1=1,
y2=2, yn = yn2+yn1, если n = 3, 4, 5, 6, ... .
Решение.
Каждый последующий элемент этой последовательности равен сумме двух предыдущих
элементов.
y1=1;
y2=2;
y3=1+2=3;
y4=2+3=5;
y5=3+5=8;
y6=5+8=13;
y7=8+13=21;
y8=13+21=34;
y9=21+34=55;
y10=34+55=89.
VI. Подведение итогов урока. Рефлексия
1. Что у вас удалось при выполнении задания?
2. Была ли работа слаженной?
3. Что не получилось, на ваш взгляд?
Тема: Числовая последовательность и способы ее задания
Основные цели и задачи урока
Образовательная: разъяснить учащимся смысл понятий последовательность, n-ый член последовательности; познакомить со способами задания последовательности.
Развивающая: развитие самостоятельности, взаимопомощи при работе в группе, сообразительности.
Воспитательная: воспитание активности и аккуратности, умение всегда видеть хорошее, привитие любви и интереса к предмету
Ожидаемые результаты освоения темы
В ходе урока приобретут новые знания о числовых последовательностях и способах ее задания. Научатся находить верное решение, составлять алгоритм решения и пользоваться им при решении заданий. Путем исследования обнаружат их некоторые свойства. Вся работа сопровождается слайдами.
Универсальные учебные действия, на формирование которых направлен образовательный процесс: умение работать в группе, развивать логическое мышление, умение анализировать, исследовать, делать выводы, отстаивать свою точку зрения. Обучить навыкам общения и сотрудничества. Использование данных технологий способствует развитию у обучающихся универсальных способов деятельности, опыта творческой деятельности, компетентности, коммуникабельности.
Ключевые идеи урока
Новые подходы в преподавании и обучении
- диалоговое обучение
- обучение тому, как обучаться
Оценивание для обучения и оценивание обучения
Обучение критическому мышлению
Обучение талантливых и одарённых детей
Тип урока
Изучение новой темы
Методы обучения
Наглядный (презентация), словесный (беседа, объяснение, диалог), практический.
Формы организации учебной деятельности уч-ся
фронтальная; групповая; парная; индивидуальная.
Используемые интерактивные методы обучения
Взаимооценивание, Самооценивание, Групповая работа, Индивидуальное работа,
Оценивания для обучения, ИКТ, Дифференцированное обучение
Применение модулей
Обучение тому, как обучаться, Обучение критическому мышлению, Оценивания для обучения, Использование ИКТ в преподавании и обучения, Обучение талантливых и одаренных детей
Оборудование и материалы
Учебник, Интерактивная доска кодоскоп, презентация, маркера, ватмат А3, линейка, цветтные карандаши, стикера, смайлики
Этапы урока
ХОД УРОКА
Прогнозируемые результаты
Создание колобративной среды
Организационный момент
(Приветствие учащихся, определение отсутствующих, проверка готовности учащихся к уроку, организация внимания).
Деление по группам.
Вступительное слово учителя
Притча “Всё в твоих руках”
Когда-то давно, в одном городе, жил великий мудрец. Слава о его мудрости разнеслась далеко вокруг его родного города, люди издалека приходили к нему за советом. Но был в городе человек, завидующий его славе. Пришел он как-то на луг, поймал бабочку, посадил ее между сомкнутых ладоней и подумал: “Пойду-ка я к мудрецу и спрошу у него: скажи, о мудрейший, какая бабочка у меня в руках- живая или мертвая? Если он скажет мертвая, я открою ладони, бабочка улетит, если он скажет живая, я сомкну ладони и бабочка умрет. Вот тогда все поймут, кто из нас умнее.” Так все и получилось. Завистник пришел в город и спросил у мудреца: “Скажи, о мудрейший, какая бабочка у меня в руках- живая или мертвая?”Тогда мудрец, который был действительно умным человеком, сказал: “Всё в твоих руках”
Полная готовность класса и оборудования урока к работе; быстрое включение класса в деловой ритм, организация внимания всех учащихся
Четко и однозначно вместе с учащимися будут сформулированы цель урока и образовательные задачи урока.
Основная часть урока
Подготовка учащихся к активному, сознательному усвоению знаний.
Какие события в нашей жизни происходят последовательно? Приведите примеры таких явлений и событий.
Ответы учеников:
дни недели,
названия месяцев,
возраст человека,
номер счёта в банке,
последовательно происходит смена дня и ночи,
последовательно увеличивает скорость автомобиль, последовательно пронумерованы дома на улице и т. д.
Задание для групп:
Работа в группах, дифференцированный подход
Каждая группа получает свое задание. После его выполнения отчитывается каждая группа перед классом, начинают ученики 1 группы.
Задание для групп:
ученикам предлагается найти закономерности и показать их с помощью стрелки.
Задание для учеников 1 и 2 групп:
1 группа:
В порядке возрастания положительные нечетные числа
1/2; 1/3; 1/4; 1/5; 1/6
В порядке убывания правильные дроби с числителем, равным 1
5; 10; 15; 20; 25;
В порядке возрастания положительные числа, кратные 5
1; 3; 5; 7; 9;
2 группа: найдите закономерности
6; 8; 16; 18; 36;
Увеличение на 3
10; 19; 37; 73; 145;
Чередовать увеличение на 2 и увеличение в 2 раза
1; 4; 7; 10; 13;
Увеличение в 2 раза и уменьшение на 1
Ответы 1 группы:
В порядке возрастания положительные нечетные числа (1; 3; 5; 7; 9;)
В порядке убывания правильные дроби с числителем, равным 1 (1/2; 1/3; 1/4; 1/5; 1/6)
В порядке возрастания положительные числа, кратные 5 (5; 10; 15; 20; 25;)
Ответы 2 группы:
1; 4; 7; 10; 13; (Увеличение на 3)
10; 19; 37; 73; 145; (Увеличение в 2 раза и уменьшение на 1)
6; 8; 16; 18; 36; (Чередовать увеличение на 2 и увеличение в 2 раза)
Изучение нового материала
- Что ты понимаешь под словом четная?
- Приведи пример?
- Теперь скажи несколько четных чисел последовательно
- А теперь расскажи нам о не четных числа?
- назови последовательные не четные числа
МОЛОДЕЦ!
Числа, образующие последовательность, называют соответственно первым, вторым, третьим, и т. д., n-ным членами последовательности.
Обозначают члены последовательности так
а1; а2; а3; а4; аn;
Последовательности могут быть конечными и бесконечными, возрастающими и убывающими.
Работа на флипчарте
хn=3n+2, то
х5=3.5+2=17;
х45=3.45+2=137.
Рекуррентный способ
Формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько), называют рекуррентной (от латинского слова recurro– возвращаться).
Например, последовательность, заданную правилом
а1=1; аn+1= аn +3
можно записать с многоточием:
1; 4; 7; 10; 13;
Физминутка 1,2,3,4,5,6,7, ...
4. Закрепление изученного материала (парная работа, дифференцированный подход)
Каждая группа получает индивидуальное задание, которое выполняют самостоятельно. При выполнении заданий ребята обсуждают решение и записывают его в тетрадь.
Даны последовательности:
аn=n4 ; аn=(-1)nn2 ; аn=n +4; аn=-n-4; аn=2n -5; аn=3n -1.
Задание для учеников 1 группы: Последовательности заданны формулами. Впишите пропущенные члены последовательности:
1; ___; 81; ___; 625; ...
-1; 4; ___; ___; -25;
5; ___; ___; ___; 9;
___; -6; ___; ___ ; -9;
___; ___; 3; 11; ___;
2; 8; ___; ___; ___;
Задание:
Выписать первые пять членов последовательности, заданной формулой своего n-ого члена.
Задание для учеников группы:
Определите, какими числами являются члены этих последовательностей, заполните таблицу.
Положительные и отрицательные числа
Положительные числа
Отрицательные числа
Работа с учебникам № 148 , № 151
Проверочная работа
1.Последовательность задана формулой an=5n+2 . Чему равен её третий член?
а) 3 б)17 в) 12 г) 22
2 . Выпишите 5 первых членов последовательности, заданной формулой an=n-3
а) -3,-2,-1,0,1 б) -2,-1,0,1,2
в) 0,-2,-4,-16,-50 г) 1,2,3,4,5
3. Найдите сумму 6-ти первых членов числовой последовательности: 2,4,6,8,
а) 66 б) 36 в) 32 г) 42
4. Какая из перечисленных последовательностей является бесконечно убывающей:
а) б) 2,4,6,8,
в) г)
Ответы: 1) б 2) б 3) г 4) г
Живое общение с учителем
Учащиеся находят ответы на поставленные вопросы.
Учащиеся учатся анализировать и делать выводы.
Формируется знание как решить систему неравенств с одной переменной
Правильные ответы в процессе диалога, общения активность ученика
Учащиеся выполняют задание
Решают самостоятельно, проверка на слайдах.
Не будут бояться ошибок, наглядно на слайдах все станет ясно.
Www. Bilimland.kz
Ученики совещаются, работая в группе, консультируются с учителем, одаренными детьми
Ученики в парной работе совещаются и находят верные решения задания
Учащиеся оценивают работу другой группы, выставляют оценку. Результаты показывают, что изученный материал усвоен.
репродуктивная деятельность ученика – это, прежде всего, воспроизводящая по определенному алгоритму деятельность школьника, которая приводит к необходимому результату.
Рефлексия
Подведение итога
Итак, мы разобрали понятие последовательности и способы ее задания.
Приведите примеры числовой последовательности: конечной и бесконечной.
Какие способы задания последовательности вы знаете.
Какая формула называется рекуррентной?
Подвести итоги урока, отметить наиболее активных учащихся. Поблагодарить учащихся за работу на уроке.
Ученики на стикерах прилепляют записи,
о том чему они научились,
что нового они узнали,
как поняли урок,
понравилось ли урок,
как они чувствовали на уроке.
Домашнее задание.
9 №150, №152
Правильные ответы в процессе диалога, активность учащихся
Затруднений при выполнении домашнего задания не будет
Атырауская область
Индерский район
село Есбол
сш им Жамбыла
учитель математики
высшего категории,
сертифицированный учитель
I-го продвинутого уровня
Искакова Светлана Сламбековна
Вида y = f (x ), x О N , где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f (n ) или y 1 , y 2 ,…, y n ,…. Значения y 1 , y 2 , y 3 ,… называют соответственно первым, вторым, третьим, … членами последовательности.
Например, для функции y = n 2 можно записать:
y 1 = 1 2 = 1;
y 2 = 2 2 = 4;
y 3 = 3 2 = 9;…y n = n 2 ;…
Способы задания последовательностей. Последовательности можно задавать различными способами, среди которых особенно важны три: аналитический, описательный и рекуррентный.
1. Последовательность задана аналитически, если задана формула ее n -го члена:
y n = f (n ).
Пример. y n = 2n – 1 – последовательность нечетных чисел: 1, 3, 5, 7, 9, …
2. Описательный способ задания числовой последовательности состоит в том, что объясняется, из каких элементов строится последовательность.
Пример 1. «Все члены последовательности равны 1». Это значит, речь идет о стационарной последовательности 1, 1, 1, …, 1, ….
Пример 2. «Последовательность состоит из всех простых чисел в порядке возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, …. При таком способе задания последовательности в данном примере трудно ответить, чему равен, скажем, 1000-й элемент последовательности.
3. Рекуррентный способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n -й член последовательности, если известны ее предыдущие члены. Название рекуррентный способ происходит от латинского слова recurrere – возвращаться. Чаще всего в таких случаях указывают формулу, позволяющую выразить n -й член последовательности через предыдущие, и задают 1–2 начальных члена последовательности.
Пример 1. y 1 = 3; y n = y n –1 + 4, если n = 2, 3, 4,….
Здесь y 1 = 3; y 2 = 3 + 4 = 7; y 3 = 7 + 4 = 11; ….
Можно видеть, что полученную в этом примере последовательность может быть задана и аналитически: y n = 4n – 1.
Пример 2. y 1 = 1; y 2 = 1; y n = y n –2 + y n –1 , если n = 3, 4,….
Здесь: y 1 = 1; y 2 = 1; y 3 = 1 + 1 = 2; y 4 = 1 + 2 = 3; y 5 = 2 + 3 = 5; y 6 = 3 + 5 = 8;
Последовательность, составленную в этом примере, специально изучают в математике, поскольку она обладает рядом интересных свойств и приложений. Ее называют последовательностью Фибоначчи – по имени итальянского математика 13 в. Задать последовательность Фибоначчи рекуррентно очень легко, а аналитически – очень трудно. n -е число Фибоначчи выражается через его порядковый номер следующей формулой .
На первый взгляд, формула для n -го числа Фибоначчи кажется неправдоподобной, так как в формуле, задающей последовательность одних только натуральных чисел, содержатся квадратные корни, но можно проверить «вручную» справедливость этой формулы для нескольких первых n .
Свойства числовых последовательностей.
Числовая последовательность – частный случай числовой функции, поэтому ряд свойств функций рассматриваются и для последовательностей.
Определение. Последовательность {y n } называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:
y 1 y 2 y 3 y n y n +1
Определение.Последовательность {y n } называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:
y 1 > y 2 > y 3 > … > y n > y n +1 > … .
Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.
Пример 1. y 1 = 1; y n = n 2 – возрастающая последовательность.
Таким образом, верна следующая теорема (характеристическое свойство арифметической прогрессии). Числовая последовательность является арифметической тогда и только тогда, когда каждый ее член, кроме первого (и последнего в случае конечной последовательности), равен среднему арифметическому предшествующего и последующего членов.
Пример. При каком значении x числа 3x + 2, 5x – 4 и 11x + 12 образуют конечную арифметическую прогрессию?
Согласно характеристическому свойству, заданные выражения должны удовлетворять соотношению
5x – 4 = ((3x + 2) + (11x + 12))/2.
Решение этого уравнения дает x = –5,5. При этом значении x заданные выражения 3x + 2, 5x – 4 и 11x + 12 принимают, соответственно, значения –14,5, –31,5, –48,5. Это – арифметическая прогрессия, ее разность равна –17.
Геометрическая прогрессия.
Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением на одно и то же число q , называют геометрической прогрессией, а число q – знаменателем геометрической прогрессии.
Таким образом, геометрическая прогрессия – это числовая последовательность {b n }, заданная рекуррентно соотношениями
b 1 = b , b n = b n –1 q (n = 2, 3, 4…).
(b и q – заданные числа, b ≠ 0, q ≠ 0).
Пример 1. 2, 6, 18, 54, … – возрастающая геометрическая прогрессия b = 2, q = 3.
Пример 2. 2, –2, 2, –2, … – геометрическая прогрессия b = 2, q = –1.
Пример 3. 8, 8, 8, 8, … – геометрическая прогрессия b = 8, q = 1.
Геометрическая прогрессия является возрастающей последовательностью, если b 1 > 0, q > 1, и убывающей, если b 1 > 0, 0 q
Одно из очевидных свойств геометрической прогрессии состоит в том, что если последовательность является геометрической прогрессией, то и последовательность квадратов, т.е.
b 1 2 , b 2 2 , b 3 2 , …, b n 2,… является геометрической прогрессией, первый член которой равен b 1 2 , а знаменатель – q 2 .
Формула n- го члена геометрической прогрессии имеет вид
b n = b 1 q n– 1 .
Можно получить формулу суммы членов конечной геометрической прогрессии.
Пусть дана конечная геометрическая прогрессия
b 1 , b 2 , b 3 , …, b n
пусть S n – сумма ее членов, т.е.
S n = b 1 + b 2 + b 3 + … + b n .
Принимается, что q № 1. Для определения S n применяется искусственный прием: выполняются некоторые геометрические преобразования выражения S n q .
S n q = (b 1 + b 2 + b 3 + … + b n –1 + b n )q = b 2 + b 3 + b 4 + …+ b n + b n q = S n + b n q – b 1 .
Таким образом, S n q = S n + b n q – b 1 и, следовательно,
Это формула суммы n членов геометрической прогрессии для случая, когда q ≠ 1.
При q = 1 формулу можно не выводить отдельно, очевидно, что в этом случае S n = a 1 n .
Геометрической прогрессия названа потому, что в ней каждый член кроме первого, равен среднему геометрическому предыдущего и последующего членов. Действительно, так как
b n = b n- 1 q;
b n = b n+ 1 /q,
следовательно, b n 2= b n– 1 b n+ 1 и верна следующаятеорема(характеристическое свойство геометрической прогрессии):
числовая последовательность является геометрической прогрессией тогда и только тогда, когда квадрат каждого ее члена, кроме первого (и последнего в случае конечной последовательности), равен произведению предыдущего и последующего членов.
Предел последовательности.
Пусть есть последовательность {c n } = {1/n }. Эту последовательность называют гармонической, поскольку каждый ее член, начиная со второго, есть среднее гармоническое между предыдущим и последующим членами. Среднее геометрическое чисел a и b есть число
В противном случае последовательность называется расходящейся.
Опираясь на это определение, можно, например, доказать наличие предела A = 0 у гармонической последовательности {c n } = {1/n }. Пусть ε – сколь угодно малое положительное число. Рассматривается разность
Существует ли такое N , что для всех n ≥ N выполняется неравенство 1/N ? Если взять в качестве N любое натуральное число, превышающее 1/ε , то для всех n ≥ N выполняется неравенство 1/n ≤ 1/N ε , что и требовалось доказать.
Доказать наличие предела у той или иной последовательности иногда бывает очень сложно. Наиболее часто встречающиеся последовательности хорошо изучены и приводятся в справочниках. Имеются важные теоремы, позволяющие сделать вывод о наличии предела у данной последовательности (и даже вычислить его), опираясь на уже изученные последовательности.
Теорема 1. Если последовательность имеет предел, то она ограничена.
Теорема 2. Если последовательность монотонна и ограничена, то она имеет предел.
Теорема 3. Если последовательность {a n } имеет предел A , то последовательности {ca n }, {a n + с} и {| a n |} имеют пределы cA , A + c , |A | соответственно (здесь c – произвольное число).
Теорема 4. Если последовательности {a n } и {b n } имеют пределы, равные A и B pa n + qb n } имеет предел pA + qB .
Теорема 5. Если последовательности {a n } и {b n }имеют пределы, равные A и B соответственно, то последовательность {a n b n } имеет предел AB.
Теорема 6. Если последовательности {a n } и {b n } имеют пределы, равные A и B соответственно, и, кроме того, b n ≠ 0 и B ≠ 0, то последовательность {a n / b n } имеет предел A/B .
Анна Чугайнова
 Ударение в английском языке
Ударение в английском языке 10 слов с ударением на 1 слог
10 слов с ударением на 1 слог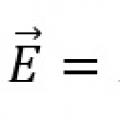 Закон Ома для замкнутой цепи и неоднородного участка цепи
Закон Ома для замкнутой цепи и неоднородного участка цепи