По своему характеру критерий гурвица. Минимаксное решение. Критерий Гурвица
В 1895 г. швейцарским ученым А. Гурвицем был предложен критерий, определяющий условия, которым должны удовлетворять коэффициенты характеристического уравнения системы для обеспечения отрицательности вещественных частей корней ее характеристического уравнения.
Приведем формулировку критерия Гурвица без доказательства. Так как характеристическое уравнение всегда может быть приведено к виду, когда а п > 0, то можно дать следующую формулировку критерия Гурвица.
Для того, чтобы система управления была устойчива, необходимо и достаточно, чтобы определитель Гурвица и все его диагональные миноры были положительными.
Если характеристическое уравнение системы я-го порядка имеет вид:
а п Х п + а я _ х я " х + ... + а } Х + я 0 =0,
то определитель Гурвица, составленный из коэффициентов характеристического уравнения, будет иметь вид:
а его диагональные миноры, определяемые из определителя Гурвица так, как показано в (6.8), будут иметь вид:
Для составления определителя Гурвица из коэффициентов характеристического уравнения я-й степени целесообразно сначала выписать по главной диагонали определителя все коэффициента уравнения от я л _, до а 0 в порядке убывания индексов коэффициентов. Затем необходимо дополнить столбцы определителя вверх и вниз от элементов главной диагонали. При дополнении столбцов вверх следует вписать в столбец коэффициенты с последовательно убывающими индексами, а при дополнении вниз - коэф-
фициенты с последовательно возрастающими индексами. На место коэффициентов, индексы которых больше чем п и меньше чем нуль, необходимо поставить нули. Условия устойчивости системы порядка п по данному критерию запишутся в виде:
а п > 0; А, > 0; Д 2 > 0 ... Д > 0; Д„>0. (6.9)
Элементы последнего столбца определителя, за исключением нижнего, будут равны нулю. Поэтому он может быть представлен в следующем виде:
Так как для устойчивой системы Д„_, > 0, то условие Д„ > 0 сводится к условию а 0 > 0.
Для получения условий нахождения системы на границе устойчивости необходимо Д п приравнять нулю, т. е. Д„ =0, соблюдая при этом условие положительности всех остальных определителей (миноров). Но условие Д п =д 0 Д„_, =0 распадается на два условия:
а 0 = 0 (6.10)
А я _,=0. (6.11)
Условие (6.10) соответствует границе устойчивости, когда характеристическое уравнение имеет нулевой корень (апериодическая граница устойчивости). Условие (6.11) соответствует границе устойчивости, когда характеристическое уравнение имеет пару чисто мнимых корней (колебательная граница устойчивости).
Значения параметров систем управления, при которых система находится на границе устойчивости, будем называть критическими значениями параметров.
Рассмотрим определение условий устойчивости для систем 1-, 2- и 3-го порядков, используя критерий устойчивости Гурви-ца. При этом считаем, что характеристическое уравнение системы приведено к виду, когда а п > 0.
1. Система управления, движение которой описывается уравнением первого порядка. Ее характеристическое уравнение имеет вид:
я,Х. + а 0 = 0.
Условия устойчивости:
д, > 0; Д, = д 0 > 0.
2. Система управления, движение которой описывается уравнением второго порядка. Ее характеристическое уравнение имеет вид:
а 2 Х 2 + а{к + д 0 = 0; д 2 >0.
Условия устойчивости:
или д, д 0 > 0, но так как д, > 0, то для того чтобы Д2 = д, д 0 >0, необходимо, чтобы д 0 > 0.
Таким образом, необходимым и достаточным условием устойчивости систем 1-го и 2-го порядков является положительность коэффициентов их характеристических уравнений, что подтверждает выводы, сделанные в предыдущем параграфе.
3. Система управления, движение которой описывается уравнением 3-го порядка. Ее характеристическое уравнение имеет вид:
д 3 А 3 + а 2 Х 2 + д,^ + д 0 =0; д 3 > 0. Условия устойчивости по Гурвицу имеют вид:
Д2 = Д 2 Д| - а ц а г >0» Д = о 0 а 2 > 0.
Так как Д 2 >0, то для выполнения последнего неравенства необходимо, чтобы д 0 > 0.
Окончательно условия устойчивости по критерию Гурвица для данной системы выглядят следующим образом:
д 3 > 0; д 2 > 0; д, > 0; д 0 > 0; д 2 д, >д 0 д 3 .
Полученный результат подтверждает ранее сделанный вывод, что положительность коэффициентов является только необходимым, но недостаточным условием устойчивости для систем третьего и выше порядков.
Рассмотрим для примера исследование устойчивости системы управления, уравнение движения которой имеет вид:
0,001 + 0,18-Р + 0,97-^- + 1,8- + 50* =
0,0015^^ + 1,5- + 10#. сИ 1 сИ
Характеристическое уравнение исследуемой системы имеет вид:
0,001Х 4 + 0,18А 3 + 0,97А. 2 + 1,8А. + 50 = 0.
Все коэффициенты характеристического уравнения положительные, поэтому необходимое условие устойчивости выполняется.
Составляем определитель Гурвица по ранее изложенному правилу:
- 0,18 1,8 0 0
- 0,001 0,97 50 0
- 0 0,18 1,8 0
- 0 0,001 0,97 50
Условия устойчивости:
- 1) Д = 0,18 > 0;
- 0,18 1,8 0,001 0,97
- 2) Д 2 =
- 3) Д, =
0,18-0,97 - 1,8 -0,001 =0,1728 > 0;
0,18 1,8 0 0,001 0,97 50 0 0,18 1,8
1,8(0,18-0,97 - 0,001 - 1,8) -
0,18 2 50 = -1,31
Следовательно, исследуемая система неустойчивая.
Применение критерия устойчивости Гурвица ограничено рядом присущих ему недостатков. Во-первых, применение этого критерия требует знания всех коэффициентов характеристического уравнения системы, т. е. всех параметров системы, что крайне неудобно при экспериментальных исследованиях систем, так как обычно характеристики рассматриваемой системы определяются из испытаний разомкнутой системы. Во-вторых, критерий устойчивости Гурвица позволяет определить, устойчива система или нет, но не позволяет определить, как следует изменить параметры системы, чтобы сделать систему устойчивой, если она неустойчивая. И, наконец, применение критерия Гурвица для системы высокого порядка связано со значительными математическими трудностями, особенно, если необходимо получить буквенный результат. Значительными достоинствами по сравнению с этим критерием обладают частотные критерии устойчивости.
Контрольные вопросы
- 1. Записать условия устойчивости по Гурвицу в общем виде для систем 5-го порядка.
- 2. Определить критическое значение передаточного коэффициента системы, передаточная функция которой в разомкнутом состоянии имеет вид:
- -. Ответ: 1с п = 122,21.
- (0,5р + 1)(0,05р + 1)(0,005 + 1) р
- 3. Исследовать устойчивость системы, характеристическое уравнение которой имеет вид: X 6 + 6А. 5 + 15Х 4 + 20А 3 + 5Х 2 + 6Х + 1 = 0. Ответ: система устойчивая.
Критерий Гурвица.
Линейная система, характеристический полином которой равен
где a 0 >0, устойчива, если положительны n главных определителей матрицы Гурвица:
 (5.8)
(5.8)
Порядок составления матрицы Гурвица следующий. На главной диагонали записываются все коэффициенты, начиная с первого. Далее заполняются строки: четными коэффициентами по порядку, если на главной диагонали стоит четный коэффициент, и нечетными, если на главной диагонали стоит нечетный коэффициент. Если какой-либо коэффициент отсутствует, то вместо него заносится нуль.
Для оценки устойчивости системы необходимо вычислить определители Гурвица D i (i = 1, 2, ... , n), которые получают из матрицы (5.8) путем отчеркивания равного числа строк и столбцов в левом верхнем углу матрицы.
Система устойчива, если D i > 0 для всех i = 1, 2, ... , n.
Последний определитель Гурвица, как видно из приведенной выше матрицы, равен
D n = a n ´ D n -1 .
Поэтому его положительность сводится при D n -1 >0 к условию a n >0,
Для систем первого и второго порядка критерий Гурвица сводится просто к положительности коэффициентов a i .
Если определитель D n =0, то система находится на границе устойчивости. Возможны два случая: апериодическая граница устойчивости, если свободный член характеристического уравнения равен нулю, что соответствует нейтрально устойчивой системе; колебательная граница устойчивости, если определитель D n -1 =0. Из условия D n -1 =0 можно определить параметры, при которых система находится на границе устойчивости.
Пример.
Передаточная функция разомкнутой системы задана в виде:  . Исследовать устойчивость системы.
. Исследовать устойчивость системы.
Решение. Характеристическое уравнение замкнутой системы
D(p)=0, где ![]() .
.
Откуда следует
Раскрыв скобки, получим
T 1 T 2 p 3 + (T 1 + T 2)p 2 + p + k = 0.
Тогда имеем: a 0 = T 1 T 2 ; a 1 = (T 1 + T 2); a 2 = 1; a 3 = k.
Коэффициенты характеристического уравнения положительны.
Составляем матрицу Гурвица
и найдем определители этой матрицы. Для устойчивости системы все они должны быть положительными:
D 1 = a 1 , откуда (T 1 + T 2) > 0;
D 2 = a 1 ´a 2 - a 0 ´a 3 , откуда (T 1 + T 2) - kT 1 T 2 > 0;
D 3 = a 1 ´a 2 ´a 3 - a 0 ´a 3 2 = a 3 (a 1 ´a 2 - a 0 ´a 3), откуда a 3 >0 , то есть k > 0.
Условие устойчивости по критерию Гурвица получает вид
(T 1 + T 2) > kT 1 T 2 или k < ( + ).
Границы устойчивости:
1) a n = 0, k = 0;
2) D n -1 = 0, k гр = ( + );
3) a 0 = 0, T 1 T 2 = 0.
Эти три границы устойчивости можно изобразить графически в пространстве параметров k, T 1 , T 2 и найти области устойчивости системы.
Найдем сначала область устойчивости системы по одному параметру k (общий коэффициент передачи разомкнутой системы). Пространство параметров здесь одна прямая линия, а границы устойчивости - точки на ней: k = 0 и k = k гр (рис.5.6). Область устойчивости лежит между этими точками.
![]()
Рис. 5.6. Область устойчивости по одному параметру
Те же границы устойчивости системы можно построить на плоскости двух параметров, например: k и T 1 (рис.5.7). Первая граница k = 0 лежит на оси T 1 . Вторая граница = k - имеет вид гиперболы с асимптотами k = 0 и k = . Третья граница T 1 = 0 совпадает с осью k. Штриховка границ сделана в сторону области устойчивости.
к.э.н., директор по науке и развитию ЗАО "КИС"
Минимаксное решение. Критерий Гурвица
Решения, принимаемые в условиях неопределенности, занимают весомую часть всего множества решений, принимаемых менеджерами. Но, как правило, на практике решения, принимаемые в условиях полной неопределенности, не встречаются. Для принятия решений предприятие должно собрать необходимый дополнительный объем релевантной информации и проанализировать ситуацию, либо принять решение на основе суждений, интуиции, анализа накопленного опыта руководителя. Для принятия оптимальных решений необходимо использовать научный подход при использовании различных методов.
К правилам принятия решений, при которых не учитывается численное значение вероятных исходов, относятся рассмотренные ранее максимаксное и максиминное решение, а также минимаксное решение и критерий Гурвица.
Минимаксное решение - это решение, при котором минимизируются максимальные потери. Это наиболее осторожный подход к принятию решений и наиболее учитывающий все возможные риски.
Правило минимакса (минимаксное правило возможных потерь ) состоит в том, чтобы для каждого решения выбрать максимально возможные потери. Затем выбирается решение, которое ведет к минимальному значению максимальных потерь.
Под потерями учитываются не только реальные потери, но и упущенные возможности. При использовании данного правила внимание уделяется возможным потерям, чем доходам.
На основании данных предыдущего примера по реализации пирожных составим таблицу возможных потерь, которая дает представление о прибылях каждого исхода, потерянных в результате принятия неправильного решения (число закупленных единиц).
Таблица возможных потерь за день
Таблица заполняется следующим образом.
Если количество закупленных пирожных равняется спросу за день, то возможные потери равняются нулю.
Если было принято решение приобрести, например, 1 пирожное, а спрос в этот день составил 2 штуки, то упущенная выгода составит 1*(60-50)=10 руб. Это и есть возможные потери. Для 2 штук пирожных, которые могли бы продать, сумма возможных потерь составляет 20 руб., для 3-х пирожных - 30 руб.
В тех случаях, когда закупленная единица не была реализована, она приносит убыток 1* (50-30)=20, это тоже возможные потери.
Для каждого решения выбирается максимальное число возможных потерь. Это числа 30, 20, 40, 60 и определяем из них минимальное 20. Данное значение соответствует решению о закупке 2 штук. Следовательно, руководствуясь правилом минимакса, минимальная величина максимальных потерь возникает в результате закупки двух пирожных в день.
Критерий Гурвица (Hurwicz criterion)- это компромиссный способ принятия решений.
При выборе решения из двух крайностей: пессимистической оценкой по критерию максимина и оптимистической оценкой максимакса рационально придерживаться промежуточной позиции, граница которой регулируется показателем пессимизма-оптимизма µ, называемым степенью оптимизма в критерии Гурвица.
В соответствии с этим компромиссным решением будет линейная комбинация минимального и максимального выигрыша
![]()
где 0 < µ < 1,
gnm - размер возможного дохода, который соответствует решениям при данных исходах.
Причем величину µ определяет исследователь или лицо, принимающее решение, при этом значению µ=1 критерию Гурвица соответствует правилу максимина (критерий Вальда), а значению µ =0 - правило максимакса (критерий Сэвиджа).
Критерий Гурвица заключается в том, что минимальному и максимальному результатам каждого решения присваивается "вес". Умножив результаты на соответствующие веса и суммируя их, лицо, принимающее решение, получает общий результат. Далее выбирается решение с наибольшим результатом.
Вернемся к предыдущему примеру и заполним таблицу по методу Гурвица.
Для четырех возможных решение были ранее получены максимаксное и максминное решения. Пусть вес минимального результата равен 0,4, следовательно, вес максимального - 0,6.

Таблица возможных решений
В данном примере критерий Гурвица свидетельствует в пользу решения о закупке одного пирожного, максимальная сумма составила 10. Очевидно, что при выборе других весов результат получается иным.
Поэтому к достоинству и одновременно недостатку критерия Гурвица относится необходимость присваивания весов возможным исходам: это позволяет учесть специфику ситуации, однако при этом всегда присутствует субъективный человеческий фактор - предпочтения аналитика.
Критерии устойчивости
Определение устойчивости АСУ по корням характеристического уравнения сопряжено с большими трудностями, связанными с решением дифференциального уравнения и большим объемом вычислений. Поэтому в практике ТАУ для определения устойчивости чаще используют критерии устойчивости.
Критерием устойчивости называется совокупность правил, методов или алгоритмов, которые позволяют судить об устойчивости АСУ без решения характеристического уравнения, используя другие признаки. Все критерии можно разделить на две группы: алгебраические критерии устойчивости и частотные критерии устойчивости. К алгебраическим критериям устойчивости относятся:
1) критерий устойчивости Вишнеградского;
2) критерий устойчивости Гурвица;
3) критерий устойчивости Рауса.
К частотным критериям устойчивости относятся:
4) частотный критерий устойчивости Найквиста;
5) частотный критерий устойчивости Михайлова.
Критерий устойчивости Гурвица можно сформулировать в форме, предложенной автором:
Если система описывается линейным дифференциальным уравнением, характеристическое уравнение которого имеет вид:
то для того, чтобы она была устойчива, т.е. чтобы все действительные корни и действительные части комплексных корней характеристического уравнения были бы отрицательны, необходимо и достаточно, чтобы все коэффициенты уравнения имели бы один и тот же знак, а диагональный детерминант порядка п-1 , составленный из коэффициентов уравнения, и все его диагональные миноры были бы положительными.
Диагональный детерминант составляется следующим образом: по диагонали определителя выписывают коэффициенты характеристического уравнения, начиная с a n -1 по а 1 . Таким образом, получается матрица, содержащая n-1 строку и n-1 столбец. Столбцы заполняют следующим образом: вверх выписывают коэффициенты с убывающими индексами, а вниз – с возрастающими. При достижении нулевого или n -го индекса далее ставят нули.
 (8.6)
(8.6)
Таким образом, получается квадратная матрица размером (n-1 )* (n-1 ), на главной диагонали которой расположены коэффициенты от a n -1 по a 1 .
Каждый диагональный минор получают из предыдущего минора путем вычеркивания последней строки и последнего столбца.
 (8.7)
(8.7)
 (8.8)
(8.8)
 (8.9)
(8.9)
D 1 =a n -1 (8.10)
Для решения вопроса об устойчивости АСУ выполняется анализ матрицы по следующим правилам:
1) если определители матрицы и всех диагональных миноров положительны, то АСУ устойчива;
2) если определитель или хотя бы один минор равен нулю, то АСУ находится на границе устойчивости;
3) если определитель или хотя бы один минор отрицательны, то АСУ неустойчива.
Рассмотрим конкретные примеры исследования систем на устойчивость с помощью критерия Гурвица.
Пример №1. АСУ включает статический объект второго порядка с передаточной функцией ![]() и интегральный регулятор с передаточной функцией . Определить при каком значении коэффициента передачи регулятора система будет устойчивой.
и интегральный регулятор с передаточной функцией . Определить при каком значении коэффициента передачи регулятора система будет устойчивой.
Запишем передаточную функцию замкнутой системы, при этом неважно по какому каналу будет записана передаточная функция, так как нас будет интересовать только знаменатель передаточной функции.
 (811)
(811)
Знаменатель передаточной функции, приравненный к нулю, является характеристическим уравнением, т.е.
![]() (8.12)
(8.12)
Подставим в уравнение (8.12) значения передаточных функций:
![]() (8.13)
(8.13)
Приводя уравнение (8.13) к общему знаменателю и приравнивая числитель к нулю, получим характеристическое уравнение для системы
Составим главный детерминант, который для данного случая имеет второй порядок:
 (8,15)
(8,15)
Из последнего равенства получим
 (8.16)
(8.16)
В уравнении (8.16) слева записан параметр настройки регулятора, а справа параметры объекта. Чтобы система была более устойчивой, необходимо иметь как можно меньшее значение коэффициента передачи регулятора. Но в этом случае регулятор будет медленно воздействовать на объект. Поэтому приходится принимать компромиссное решение: чтобы система была устойчивой и регулятор достаточно быстро воздействовал на объект.
Если в уравнении (8.16) поставить знак равенства, т.е.  , то система окажется на границе устойчивости. Если
, то система окажется на границе устойчивости. Если  , то система будет неустойчивой. Поскольку параметры объекта изменяются довольно медленно, то воздействовать на характер переходного процесса можно, изменяя параметры регулятора.
, то система будет неустойчивой. Поскольку параметры объекта изменяются довольно медленно, то воздействовать на характер переходного процесса можно, изменяя параметры регулятора.
Коэффициент передачи регулятора, при котором система оказывается на границе устойчивости, называется критическим.
Условие (8.17) можно записать и так
![]() (8.18)
(8.18)
Уравнение (8.18) перепишем в форме
Уравнение (8.19) является уравнением гиперболы Вышнеградского, который сформулировал критерий устойчивости для систем, описываемых уравнениями не выше третьего порядка.
При переходе от уравнения (8.18) к уравнению (8.19) необходимо соблюдать следующие правила:
1) параметры X и Y должны быть безразмерными;
2) параметр X должен быть пропорционален коэффициенту передачи регулятора.
![]()
![]()
![]() (8.20)
(8.20)
Построим гиперболу Вышнеградского в полученных координатах (рис. 8.4).

Рисунок 8.4 – Гипербола Вышнеградского для систем третьего порядка
Пример №2. Рассмотрим задачу, сформулированную в примере №1, но для случая, когда объект имеет передаточную функцию вида
![]()
Приравняв в уравнении (8.14) Т 2 к нулю, получим характеристическое уравнение
![]() (8.22)
(8.22)
Составим главный детерминант, который для данного случая имеет первый порядок:
Получено условие, которое выполняется при любых параметрах системы.
Системы, которые при определенных значениях своих параметров могут быть устойчивыми, называются структурно-устойчивыми.
Пример №3. АСУ включает астатический объект второго порядка с передаточной функцией ![]() и интегральный регулятор с передаточной функцией . Определить, при каком значении коэффициента передачи регулятора система будет устойчивой.
и интегральный регулятор с передаточной функцией . Определить, при каком значении коэффициента передачи регулятора система будет устойчивой.
Используя уравнение (8.13) и подставляя в него значения передаточных функций, получим
![]() (8.23)
(8.23)
![]() (8.24)
(8.24)
Перепишем уравнение (8.24) следующим образом:
Тогда главный детерминант примет вид:

В данном случае главный детерминант отрицательный, т.е. система неустойчивая, при этом она неустойчивая при любых своих параметрах. О таких системах говорят, что она структурно-неустойчивая.
Из последнего примера можно сделать вывод: что интегральный регулятор нельзя устанавливать на астатическом объекте, так как в любом случае мы получим неустойчивую систему.
Несмотря на простоту применения критерия Гурвица, он обладает рядом недостатков:
1) необходимо рассматривать передаточную функцию замкнутой системы, которая получается достаточно сложной;
2) с помощью критерия можно анализировать системы, у которых в знаменателе передаточной функции стоит рациональный многочлен.
Действительно, если передаточная функция объекта ![]() , а регулятора , то характеристическое уравнение имеет вид:
, а регулятора , то характеристическое уравнение имеет вид:
С помощью критерия устойчивости Гурвица эту систему исследовать нельзя. В этом случае нужны другие критерии.
Обычный (или простой) критерий Гурвица учитывает только крайние исходы x i max и x i min каждой альтернативы:
x i max = max (x ij ) , x i min = min (x ij ) , j = 1..M
Он позволяет учесть субъективное отношение применяющего данный критерий ЛПР за счет придания этим исходам разных "весов". Для этого в расчет критерия введен "коэффициент оптимизма" λ, 0 ≤ λ ≤ 1 . Формула для расчета критерия Гурвица для i -й альтернативы с коэффициентом оптимизма λ выглядит следующим образом:
H i (λ) = λ x i max + (1 - λ) x i min
Если исходы представляют возможные выигрыши, то оптимальной признается альтернатива с максимальным значением критерия Гурвица:
Х* = Х k , H k (λ) = max (H i (λ) ) , i = 1..N
Как видно из формулы, правильный выбор коэффициента оптимизма λ оказывает существенное влияние на результат применения критерия. Остановимся подробнее на логике подбора λ .
Если ЛПР настроен пессимистически, то для него важнее меньше потерять при плохом развитии событий, пусть даже это означает не такой большой выигрыш при удачном состоянии. Значит, удельный вес наихудшего исхода x i min в оценке альтернативы должен быть выше, чем для x i mах . Это обеспечивается, когда λ находится в пределах от 0 до 0.5 , исключая последнее значение.
При λ = 0 критерий Гурвица "вырождается" в критерий Вальда и подходит только для очень пессимистично настроенных ЛПР.
Оптимистичный ЛПР, напротив, ориентируется на лучшие исходы, так как для него важнее больше выиграть, а не меньше проиграть. Больший удельный вес в оценке наилучшего исхода достигается при λ больше 0.5 и до 1 включительно. При λ = 1 критерий Гурвица становится критерием "максимакса", который учитывает исключительно наибольший исход каждой альтернативы.
Если у ЛПР нет ярко выраженного уклона ни в сторону пессимизма, ни оптимизма, коэффициент λ принимается равным 0.5 .
Пример применения критерия Гурвица
В условиях задачи из п.2.7 (табл.2.2) рассмотрим принятие решения по критерию Гурвица для ЛПР, настроенного оптимистически (λ = 0.8 ), и ЛПР-пессимиста (λ = 0.3 ). Порядок действий таков:
1. Найдем максимальные x i max и минимальные x i min исходы для каждого проекта:
x 1 max = max (45, 25, 50) = 50 x 1 min = min (45, 25, 50) = 25
x 2 max = max (20, 60, 25) = 60 x 2 min = min (20, 60, 25) = 20
2. Рассчитаем величину критерия Гурвица при заданных значениях коэффициента оптимизма:
ЛПР-оптимист (λ=0.8 ):
H 1 (0.8) = λ x 1 max + (1 - λ) x 1 min = 0.8×50 + (1 - 0.8) ×25 = 45
H 2 (0.8) = λ x 2 max + (1 - λ) x 2 min = 0.8×60 + (1 - 0.8) ×20 = 52
ЛПР-пессимист (λ=0.3 ):
H 1 (0.3) = λ x 1 max + (1- λ) x 1 min = 0.3×50 + (1 - 0.3) ×25 = 32.5
H 2 (0.3) = λ x 2 max + (1- λ) x 2 min = 0.3×60 + (1 - 0.3) ×20 = 32
3. Сравним полученные величины. Оптимальными для каждого ЛПР будут альтернативы с максимальным значением критерия Гурвица:
ЛПР-оптимист (λ = 0.8 ):
45 < 52 => H 1 (0.8) < H 2 (0.8) => X* = X 2
ЛПР-пессимист (λ = 0.3 ):
32.5 < 32 => H 1 (0.3) > H 2 (0.3) => X* = X 1
Как мы видим, выбор оптимальной альтернативы в одних и тех же условиях существенным образом зависит от отношения ЛПР к риску. Если для пессимиста оба проекта примерно равноценны, то оптимист, который надеется на лучшее, выберет второй проект. Его высокая наилучшая прибыль (60 ) при больших значениях коэффициента λ значительно повышает ценность данного проекта по критерию Гурвица.
 10 слов с ударением на 1 слог
10 слов с ударением на 1 слог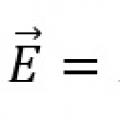 Закон Ома для замкнутой цепи и неоднородного участка цепи
Закон Ома для замкнутой цепи и неоднородного участка цепи Чиновники-академики уволены с госслужбы
Чиновники-академики уволены с госслужбы