Средняя по способу моментов. Свойства средней арифметической и расчет ее способом моментов. Виды средних и способы их вычисления
Вариационные ряды распределения состоят их двух элементов вариантов и частот.
Вариантами называются числовые значения колличественного признака в ряду распределения, они могут быть положительными и отрицательными, абсолютными и относительными. Частоты – это численности отдельных вариантов или каждой группы вариационного ряда. Сумма всех частот называется объемом совокупности и определяет число элементов всей совокупности.
Ряды распр-я могут быть образованы по качественному(атрибутивному) и колич-му пр-ку. В первом случае они наз. атрибутивными,а во втором- вариационными.
Вариационные ряды распр-ия по сп-бу постр-ия бывают дискретные и интервальные:
Дискр. вариац. ряд распр-я - группы сост-ны по признаку, изменяющемуся дискретно и приним-му только целые значения. Интервальный вариац. ряд распр-ия - группировачный признак, сост-ий групп-ки, может принимать в опред-ом интервале любые знач-ия. Число ед-ц частоты, приходящиеся на ед-цу инт-ла наз. плотностью распред-я . Ряд накопл-ых частот (кумулятивный)-показ-т число случаев ниже или выше опред-го уровня. Графич изображения ряда распред.: линейные, плоскостные диаграммы, гистограммы, куммулятивная кривая (изображ-ет ряд накопл-х частот)
9. Средняя арифметическая взвешенная.
При расчете средних величин отдельные значения признака, который осредняется, могут повторяться, поэтому расчет средней величины производится по сгруппированным данным. В этом случае речь идет об использовании средней арифметической взвешенной, которая имеет вид: X средн = (EXi*fi)/ Efi
При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам.
Расчет средней по способу моментов. Основан на свойствах средней арифметической. В качестве условного ноля – X0 выбирают середину одного из центральных интервалов, обладающего наибольшей частотой.Этот способ используется только в рядах с равными интервалами.
10. Средняя гармоническая простая и взвеш.
Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1. Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1:
К примеру, нам нужно вычислить среднюю
скорость двух автомашин, прошедших один
и тот же путь, но с разной скоростью:
первая - со скоростью 100 км/ч, вторая - 90
км/ч. Применяя метод средней гармонической,
мы вычисляем среднюю скорость:
примеру, нам нужно вычислить среднюю
скорость двух автомашин, прошедших один
и тот же путь, но с разной скоростью:
первая - со скоростью 100 км/ч, вторая - 90
км/ч. Применяя метод средней гармонической,
мы вычисляем среднюю скорость:
В статист практике чаще исп гармонич взвеш , формула кот имеет вид:
Данная формула используется в тех случаях, когда веса (или объемы явлений) по каждому признаку не равны. В исходном соотношении для расчета средней известен числитель, но неизвестен знаменатель.
Например, при расчете средней цены мы должны пользоваться отношением суммы реализации к количеству реализованных единиц. Нам не известно количество реализованных единиц (речь идет о разных товарах), но известны суммы реализаций этих различных товаров. Допустим, необходимо узнать среднюю цену реализованных товаров: Вид товара Цена за единицу, руб.Сумма реализаций, руб.
П олучаем
олучаем
Е![]() сли
здесь использовать формулу средней
арифметической, то можно получить
среднюю цену, которая будет нереальна:
сли
здесь использовать формулу средней
арифметической, то можно получить
среднюю цену, которая будет нереальна:
11. Упрощенный расчет средней арифм. (ср. ар.) (способ моментов).
Пользуясь св-ми ср. ар., ее можно рассчитать след. образом: 1) вычесть из всех вариант постоянное число (лучше значение серединной варианты); 2) разделить варианты на постоянное число – на величину интервала; 3) частоты выразить в %. Вычисление ср. ар. первыми двумя способами называется способом отсчета от условного начала (способом моментов). Этот способ применяется в рядах с разными интервалами. Ср. ар. в этом случае опред. по ф-ле:
 Где m
– момент первого порядка; х 0
– начало отсчета; К – величина интервала.
Где m
– момент первого порядка; х 0
– начало отсчета; К – величина интервала.
12. Мода и медиана.
Д ля
определения структуры совокупности
используют особые средние показатели,
к которым относятся медиана и мода, или
так называемые структурные средние.
Медиана
(Ме)
- это величина, которая соответствует
варианту, находящемуся в середине
ранжированного ряда. Для ранжированного
ряда с нечетным числом индивидуальных
величин (например, 1, 2, 3, 3, 6, 7, 9, 9, 10)
медианой будет величина, которая
расположена в центре ряда, т.е. пятая
величина. Для ранжированного ряда с
четным числом индивидуальных величин
(например, 1, 5, 7, 10, 11, 14) медианой будет
средняя арифметическая величина, которая
рассчитывается из двух смежных величин.
Для нашего случая медиана равна (7+10) :
2= 8,5. То есть для нахождения медианы
сначала необходимо определить ее
порядковый номер (ее положение в
ранжированном ряду) по формуле Nme=(n+1)/2,
где n - число единиц в совокупности.
Численное значение медианы определяют
по накопленным частотам в дискретном
вариационном ряду. Для этого сначала
следует указать интервал нахождения
медианы в интервальном ряду распределения.
Медианным называют первый интервал,
где сумма накопленных частот превышает
половину наблюдений от общего числа
всех наблюдений. Численное значение
медианы обычно определяют по формуле-----
где xМе - нижняя
граница медианного интервала; i - величина
интервала; S-1 - накопленная частота
интервала, которая предшествует
медианному; f - частота медианного
интервала.
ля
определения структуры совокупности
используют особые средние показатели,
к которым относятся медиана и мода, или
так называемые структурные средние.
Медиана
(Ме)
- это величина, которая соответствует
варианту, находящемуся в середине
ранжированного ряда. Для ранжированного
ряда с нечетным числом индивидуальных
величин (например, 1, 2, 3, 3, 6, 7, 9, 9, 10)
медианой будет величина, которая
расположена в центре ряда, т.е. пятая
величина. Для ранжированного ряда с
четным числом индивидуальных величин
(например, 1, 5, 7, 10, 11, 14) медианой будет
средняя арифметическая величина, которая
рассчитывается из двух смежных величин.
Для нашего случая медиана равна (7+10) :
2= 8,5. То есть для нахождения медианы
сначала необходимо определить ее
порядковый номер (ее положение в
ранжированном ряду) по формуле Nme=(n+1)/2,
где n - число единиц в совокупности.
Численное значение медианы определяют
по накопленным частотам в дискретном
вариационном ряду. Для этого сначала
следует указать интервал нахождения
медианы в интервальном ряду распределения.
Медианным называют первый интервал,
где сумма накопленных частот превышает
половину наблюдений от общего числа
всех наблюдений. Численное значение
медианы обычно определяют по формуле-----
где xМе - нижняя
граница медианного интервала; i - величина
интервала; S-1 - накопленная частота
интервала, которая предшествует
медианному; f - частота медианного
интервала.
Модой (Мо) называют значение признака, которое встречается наиболее часто у единиц совокупности. Для дискретного ряда модой будет являться вариант с наибольшей частотой. Для определения моды интервального ряда сначала определяют модальный интервал (интервал, имеющий наибольшую частоту). Затем в пределах этого интервала находят то значение признака, которое может являться модой. Чтобы найти конкретное значение моды, необходимо использовать формулу

где xМо - нижняя граница модального интервала; iМо - величина модального интервала; fМо - частота модального интервала; fМо-1 - частота интервала, предшествующего модальному; fМо+1 - частота интервала, следующего за модальным.
Мода имеет широкое распространение в маркетинговой деятельности при изучении покупательского спроса, особенно при определении пользующихся наибольшим спросом размеров одежды и обуви, при регулировании ценовой политики.
13. Свойства средней ариф. (ср. ар.)
1.Если
из всех вариантов ряда (-) или ко всем
вариантам (+) постоянное число, то ср.
ар. соответственно уменьшится или
увеличится на это число.
 .2.Если
все варианты ряда умножить или разделить
на постоянное число, то ср. ар. соответственно
увеличится или уменьшится в это число
раз.
.2.Если
все варианты ряда умножить или разделить
на постоянное число, то ср. ар. соответственно
увеличится или уменьшится в это число
раз.
 3.Если
все частоты увеличить или уменьшить в
постоянное число раз, то средняя от
этого не изменится.
3.Если
все частоты увеличить или уменьшить в
постоянное число раз, то средняя от
этого не изменится.
 .
.
4.Сумма
отклонений всех вариантов ряда от ср.
ар. = 0. (Нулевое свойство средней).
.
5. Σf i =Σfix i
.
Произведение
средней на сумму частот всегда равно
сумме произведений вариант на частоты.
Σf i =Σfix i
.
Произведение
средней на сумму частот всегда равно
сумме произведений вариант на частоты.
6.Сумма квадратов отклонений всех вариантов ряда от ср. ар.
Данное св-во положено в основу метода наименьших квадратов, кот. широко применяется в исследовании стат. взаимосвязей.
14. Виды дисперсий. Правило их сложения .
Р азличают
три вида дисперсий: общая; средняя
внутригрупповая; межгрупповая. Общая
дисперсия (
2
о
)
характеризует вариацию признака всей
совокупности под влиянием всех тех
факторов, которые обусловили данную
вариацию. Эта величина определяется по
формуле 2
о = (X
– Xо
средн) 2 *f
/ f,
где Xо
средн - общая средняя арифметическая
всей исследуемой совокупности. Средняя
внутригрупп дисперс
(
2
средн
) свидетельствует
о случайной вариации, которая может
возникнуть под влиянием каких-либо
неучтенных факторов и которая не зависит
от признака-фактора, положенного в
основу группировки. Данная дисперсия
рассчитывается следующим образом:
сначала рассчитываются дисперсии по
отдельным группам (
2
i
),
затем рассчитывается средняя
внутригрупповая дисперсия (
2
i
cредн):
где ni - число единиц в группе. Межгрупповая
дисперсия
характеризует
систематическую вариацию, т.е. различия
в величине исследуемого признака,
возникающие под влиянием признака-фактора,
который положен в основу группировки.
Эта дисперсия рассчитывается по формуле
азличают
три вида дисперсий: общая; средняя
внутригрупповая; межгрупповая. Общая
дисперсия (
2
о
)
характеризует вариацию признака всей
совокупности под влиянием всех тех
факторов, которые обусловили данную
вариацию. Эта величина определяется по
формуле 2
о = (X
– Xо
средн) 2 *f
/ f,
где Xо
средн - общая средняя арифметическая
всей исследуемой совокупности. Средняя
внутригрупп дисперс
(
2
средн
) свидетельствует
о случайной вариации, которая может
возникнуть под влиянием каких-либо
неучтенных факторов и которая не зависит
от признака-фактора, положенного в
основу группировки. Данная дисперсия
рассчитывается следующим образом:
сначала рассчитываются дисперсии по
отдельным группам (
2
i
),
затем рассчитывается средняя
внутригрупповая дисперсия (
2
i
cредн):
где ni - число единиц в группе. Межгрупповая
дисперсия
характеризует
систематическую вариацию, т.е. различия
в величине исследуемого признака,
возникающие под влиянием признака-фактора,
который положен в основу группировки.
Эта дисперсия рассчитывается по формуле
г де
- средняя величина по отдельной группе.
Все три вида дисперсии связаны между
собой: общая дисперсия равна сумме
средней внутригрупповой дисперсии и
межгрупповой дисперсии:
де
- средняя величина по отдельной группе.
Все три вида дисперсии связаны между
собой: общая дисперсия равна сумме
средней внутригрупповой дисперсии и
межгрупповой дисперсии:
Данное соотношение отражает закон, который называют правилом сложения дисперсий. Согласно этому закону (правилу), общая дисперсия, которая возникает под влиянием всех факторов, равна сумме дисперсий, которые появляются как под влиянием признака-фактора, положенного в основу группировки, так и под влиянием других факторов. Благодаря правилу сложения дисперсий можно определить, какая часть общей дисперсии находится под влиянием признака-фактора, положенного в основу группировки.
15 . Виды средних. Их исчисление .

16. Показатели вариации, применяемые в статистике.
Вариация, т.е. несовпадение уровней одного и того же показателя у разных объектов, имеет объективный характер и помогает познать сущность изучаемого явления. Для измерения вариации в статистике применяют несколько способов. Наиболее простым явл расчет показателя размаха вариации Н как разницы между Xmax и Xmin: H=Xmax - Xmin. Но размах вариации показывает лишь крайние значения признака. Повторяемость промежуточных значений здесь не учитывается. Среднее линейное отклонение d - среднее арифметическое значение абсолютных отклонений признака от его среднего уровня: d = (Xi – X средн) / n. При повторяемости отдельных значений Х используют формулу средней арифметической взвешенной. В статистических научных исследованиях для измерения вариации чаще всего применяют показатель дисперсии: δ = (Xi – X средн) 2 / n. Показатель s, равный √δ 2 , называется средним квадратическим отклонением. Величина Mx = √(δ 2 /n)-средняя ошибка выборки и явля хар-кой отклонения выборочного среднего значения призн от его истинной средней величины. Показатель средней ошибки использ при оценке достоверности результатов выборочн наблюд. Коэфф осцилляции отражает относит колеблемость крайних значений признака вокруг средней: Ko = (R/X средн)*100%. Относительное линейное отключение характеризует долю усредненного значения признака абсолютных отклонений от средней величины Kd = (d средн/ X средн)*100%. Коэффициент вариации: V = (δ/X средн)*100%
17. Простейшие приёмы обработки рядов динамики.
Простейшими видами обработки рядов динамики являются: укрупнение интервалов, метод скользящей средней, аналитическое выравнивание, экстраполяция и интерполяция.
Укрупнение интервалов. Ряд динамики разделяют на достаточно большое число равных интервалов. Если средн уровни по интервалам не позволяют увидеть тенденцию разв, переходят к расчету уровней за большие промежутки времени, увеличивая длину каждого интервала (уменьшая количество интервалов). Скользящая средняя. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Целое число уровней, по которым рассчитывается среднее значение, называют интервалом сглаживания. Для того чтобы создать модель, выражающую основную тенденцию изменения уровней динамического ряда во времени, используется аналитическое выравнивание ряда динамики. Простейшими моделями, выражающими тенденцию развития, являются: линейная функция прямой, показательная функция, парабола, парабола n-порядка, гипербола, экспонента. Иногда возникает необходимость предвидеть будущий уровень ряда динамики. В таких случаях прибегают к приему обработки рядов динамики, называемому экстраполяцией : y n +1 = y n + ∆y n +∆∆y n , где y n +1 - неизвестный уровень ряда, y n - последний известный уровень ряда, ∆y n - цепной абсолютный прирост последнего уровня ряда (∆y n = y n - y n -1), ∆∆y n - изменение прироста последнего уровня ряда. Наряду с экстраполяцией иногда применяется такой прием обработки рядов динамики, как интерполяция - искусственное нахождение отсутствующих членов внутри динамического ряда. Неизвестный уровень ряда находится по формуле: y i = (y i +1 + y i -1) / 2. Где: y i - неизвестный уровень ряда, y i +1 - последующий за неизвестным уровень ряда, y i -1 - предыдущий уровень ряда.
Формулы по статистике
Тема 1: Группировка статистических данных
Определение числа групп (если группи-ка по непрер. приз-ку или дискрет. со многими знач-ями)
Определение величины равного интервала :
Тема 2: Абсолютные и относительные величины
Относительные величины :
1) относит. вел-на структуры :
2) относит. вел-на планового задания :
3) относит. вел-на выполнения плана :
4) относит. вел-на динамики или темп роста :
![]()
5) относит. вел-на сравнения
6) относит. вел-на интенсивности (пример: фондоотдача = объем/стоимость (один год))
Тема 3: Средние величины и показатели вариации
Средняя арифметическая
простая :
взвешенная :
Средняя гармоническая
простая :
взвешенная : , сумма значений признака по группе
Свойства средн. арифметической:
если каждую вари-ту х умен-ть или увел-ть на одно и то же число, то ср. вел-на умен-ется или увел-ется на это же число;
если каждую вари-ту х умен-ть или увел-ть в одно и то же число раз, то ср. вел-на умен-ется или увел-ется в одно и то же число раз;
если каждую частоту f умен-ть или увел-ть в одно и то же число раз, то ср. вел-на не изменится.
Ср. вел-на зависит от вар-ты х и структуры совок-сти , кот. харак-ется долями d .
Ряд распределения имеет 3 центра :
1) ср. аримет-кое ;
2) мода – наиболее часто встречающаяся вар-та ;
3) медиана – вар-та, стоящая в середине ряда распре-ния. Сначала находят N медианы, кот. равен n/2, если число еди-ц совок-сти n – чётное, или , если число еди-ц совок-сти нечетное .
Осн. пока-ли вариации :
1)
размах
вариации
:
![]()
2) ср. линейное отклонение (ср. арифм-кая из абсолют. откл-ний отдел. значений)
Для несгруппир. данных:
Для
сгруппир. данных:
![]()
3) ср. квадратическое отклонение (хар-ет ср. абсол. откл-ние вар-ты от ср. вел-ны)
Для
несгруппир. данных
:

Для
сгруппир. данных
:

4) Дисперсия – квадрат среднеквадр-ного откл-ния
Для
несгруппир. данных
:
![]()
Для
сгруппир. данных
:
![]()
Общая
дисперсия:
![]() (для сгрупп.)
(для сгрупп.) ![]() (для несгрупп.)
(для несгрупп.)
– ср. вел-на резул. приз-ка в сово-сти, - частота (в совокупности!)
Внутригрупповая
дисперсия:
![]() - кол-во вариант в группе i
- кол-во вариант в группе i
Междугрупповая
дисперсия:
![]() - кол-во вариант в группе i
- кол-во вариант в группе i
Правило
сложения дисперсий:
![]()
Не имеет еди-ц измерения.
5) Коэффициент вариации хар-ет ср. относит. откл-ние вар-ты от ср. вел-ны.
Способ моментов
Часто мы сталкиваемся с расчетом средней арифметической упрощенным способом.
В этом случае используются свойства средней величины. Метод упрощенного расчета называется способом моментов, либо способом отсчета от условного нуля.
Способ моментов предполагает следующие действия :
1) Выбирается начало отсчета (из х ) – условный нуль (A ). Обычно как можно ближе к середине распре-ния.
2) Находятся отклонения вариантов от условного нуля ().
4) Если эти отклонения содержат общий множитель (k ), то рассчитанные
отклонения делятся на этот множитель.
Способ моментов :

Средняя:
![]()
Дисперсия:
![]()
Тема 4: Выборочное наблюдение
Обозначения в теории выборки:
|
N – числи-ль генер. выборки |
n – числи-ль генер. выборки |
|
Генер. средняя (оценивают) |
– выбор. средняя (рассчитывают) |
|
p – генер. доля (оценивают) |
w – выбор. доля (рассчитывают) |
|
P (t ) – задаваемый уровень веро-сти |
|
Генер. средняя: с задан. уровнем вероя-сти P(t)
– ошибка выборки для ср. вел-ны
, t – критерий надеж-сти, его вел-на зав-т от уровня задан. вероя-сти P(t)
Если 1) P (t ) = 0,683, то t =1 ; 2) P (t ) = 0,954, то t =2 ; 3) P (t ) = 0,997, то t =3
– среднеквадр. ошибка выборки
– верна для повторного отбора в выборке.
 - для бесповторного отбора
- для бесповторного отбора
Доказано: с задан. уровнем вероя-сти P(t)
– ошибка выборки для доли
, – среднеквадр. ошибка выборки для доли
 –для повторного отбора
–для повторного отбора
 - для бесповторного отбора
- для бесповторного отбора
Тема 5: Ряды динамики
Аналит. пока-ли:
1) Абсолют. прирост (разница уровней)
(цепной) ; (базисный)
2) Темп роста (отношение уровней)
(цепной) ; (базисный)
3) Темп прироста
![]() (цепной) ;
(цепной) ; ![]() (базисный)
(базисный)
4) Абсолютное значение 1% прироста
![]() (цепной) ;
(цепной) ; ![]() (базисный)
(базисный)
Средние показатели:
1) ср. уровни динам. ряда ;
2) ср. аналитич. показ-ли динам. ряда .
Расчет ср. уровня зав-т от вида РД:
а) для интерв. РД с равн. периодами вре-ни – ср. арифмет. простая
б) для интерв. РД с неравн. периодами вре-ни – ср. арифмет. взвешенная
в) для моментных РД с равноотстоящими датами – ср. хронологическая
г) для моментных РД с неравноотстоящими датами – ср. арифмет. взвешенная
Расчет ср. аналит. показ-лей:
а)
ср.
абсолют. прирост
![]()
б) ср. темп роста
в)
ср.
темп прироста
![]()
Смыкание РД
Для проведения смыкания РД в смыкаемых рядах находится временной момент (дата, период), когда им-ся сведения об изучаемом признаке как в прежних, так и в новых условиях. Рассчитывается коэфф-т, дальнейш. расчеты – по сомкнутом. ряду.
В ходе обработки РД важн. задачей яв-ся выявление основ. тенденции раз-тия явления (тренда) и сглаживание случ. колебаний. Для решения этой задачи сущ-ют особые способы, кот. наз-ют методами выравнивания.
3 основн. способа обработки динамического ряда:
а) укрупнение интервалов РД и расчет средних для кажд. укрупненного интервала;
(переход от менее продолжит.инт-лов к более продолжит. Средняя, рассчитанная по укрупненным инт-лам, позволяет выявить направление и характер (ускорение или замедление) основ. тенденции развития. Средняя рассчитывается по формулам простой средней арифметической.
б) метод скользящей средней;
(вычисл-ся ср. уровень из опред. числа, обычно нечетного, первых по счету уровней ряда. Затем - из такого же числа уровней, но начиная со второго по счету, далее - начиная с третьего и т. д. Т/о, средняя как бы «скользит» по временному ряду от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий.
в) аналитическое выравнивание.
Сезонные колебания и волны
Индексами сезонности яв-ся процентные отношения фактических внутригодовых уровней к постоянной или переменной средней. Совокупность этих показателей отражает сезонную волну.
Для выявления сезон. колебаний обычно испо-ют данные за несколько лет, распределенные по месяцам. Для каждого месяца рассчитывается средняя величина уровня, например за 3 года ( ), затем из них вычисляется средний уровень для всего ряда ( ), далее определяется процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда:
![]()
где - средний уровень для каждого месяца;
Среднемесячный уровень для всего ряда.
Для наглядного представления сезонной волны индексы сезонности изображают в виде графиков.
Индивидуальные индексы:
|
себестоимости |
стоимости |
денежных затрат |
затрат труда |
||
|
i q |
i p |
i z |
i pq |
i qz |
i qt |
Общие индексы:
|
Общий индекс физического объема (как в среднем изм-лось кол-во товаров на рынке) | |
|
Абсолютное изм-ние стои-сти за счет изм-ния кол-ва товаров |
|
|
Общий индекс цен (агрегатный) (как в среднем изм-лись цены на рынке) | |
|
Абсолютное изм-ние стои-сти за счет изм-ния цен |
|
|
Общий индекс товарооборота (стоимости) общ. относит. изме-ния стои-сти товаров на рынке |
|
|
Общ. абсолют. изм-ние стои-сти товаров на рынке |
|
|
Взаимосвязь индексов |
I pq = I p I q |
|
Общий индекс себестоимости | |
|
Общий индекс физич. объема (по себестоимости) | |
|
Взаимосвязь между индексами | |
|
Общий индекс затрат на производство |
1.имеется абстрактный характер так как является обобщающей величиной, в ней стираются
случайные колебания
2.занимает срединное положение в ряду (в строго симметричном ряду)
3.сумма отклонений всех вариант от средней величины равна нулю. Данное свойство средней
величины используется для проверки правильности расчета средней величины.
Виды средних величин
1. Мода (Мо) - варианта, наиболее часто встречающая и в вариационном ряду.
2. Медиана (Ме) - варианта занимающая в вариационном ряду срединное
положение, т.е., центральная варианта, делящая вариационный ряд на две
равные части.
М о и М е - условные средние.
3. Средняя арифметическая:
а).Средняя арифметическая простая
б).Средняя арифметическая взвешенная
в). Средняя арифметическая, вычисленная по способу моментов.
Вычисление средней арифметической, простой и взвешенной
В случаях, когда мы имеем простой вариационный ряд, в котором каждой варианте
соответствует частота (Р) равная 1, вычисляется средняя арифметическая простая по
где М средняя арифметическая - знак суммирования V - варианта, n - число наблюдений
Таким образом, средняя арифметическая простая равна сумме всех вариант, деленной на число
наблюдений.
Пример: Определение средней массы тела юношей в возрасте 18 лет (в кг)
Однако чаще всего приходится вычислять среднюю арифметическую взвешенную, которая
получается из взвешенных рядов, где
каждая варианта встречается
различное количество раз
встречается
различное количество раз
или, как говорят, имеет различный вес.
Средняя арифметическая взвешенная вычисляется по формуле:
М = VР ,
n где М средняя арифметическая - знак суммирования, V - варианта,
Р -частота встречаемости, n - число наблюдений
Таким образом, средняя арифметическая взвешенная равна сумме произведений вариант на их
частоты, деленной на число всех наблюдений.
Пример: определение средней массы тела юношей в возрасте 18 лет (в кг.)
|
|
|||
Вычисление средней арифметической по способу моментов
При большом числе наблюдений или при большом числовом значении вариант применяют
упрощенный способ вычисления средней арифметической- способ моментов.
М = А+ i ар
где М - средняя арифметическая; А - условная средняя; i - интервал между группами вариант;
- знак суммирования.; а- условное отклонение каждой варианты от условной средней;
р - частота встречаемости вариант; n - число наблюдений.
Пример вычисления средней арифметической по способу моментов (средней массы тела
юношей в возрасте 18 лет)
|
ар = - 10кг |
Этапы расчета средней по способу моментов:
2) определяем "а" - условное отклонение варианты от условной средней, для этого из каждой варианты вычитаем условную среднюю: а = V - А, (например, а = 64 - 62 = +2 и т.д.).
3) умножаем условное отклонение "а" на частоту "р" каждой варианты и получаем произведение а р;
4) находим сумму а. р = - 10кг
5) рассчитываем среднюю арифметическую по способу моментов:
М = А + i аР = 62 - 10,4 = 61,6кг
Таким образом, можно сделать вывод, что в изучаемой нами группе юношей средняя масса тела
Средняя арифметическая сама по себе ничего не говорит о том вариационном ряде, из которого
она была вычислена. На ее типичность (достоверность) влияет однородность рассматриваемого
материала и колеблемость ряда.
Пример: даны два одинаковых по числу наблюдений вариационных ряда, в которых
представлены данные измерений окружности головы детей в возрасте от 1 года до 2-х лет
Имея одинаковое число наблюдений и одинаковые средние арифметические (М= 46 см), ряды
имеют различия в распределении внутри. Так варианты первого ряда отклоняются в целом от
средней арифметической с меньшим значением, чем варианты второго ряда, что дает
возможность предположить, что средняя арифметическая (46 см) более типична для первого
ряда, чем для второго.
В статистике для характеристики разнообразия вариационного ряда употребляют среднее
квадратическое отклонение ()
Существует два способа расчета среднего квадратического отклонения: среднеарифметический
способ и способ моментов. При среднеарифметическом способе расчета применяют формулу:

где d истинное отклонение каждой варианты от истиной средней М. Формула используется при
небольшом числе наблюдений (п 30)
Формула для определения по способу моментов:

где а - условное отклонение варианты
от условной средней
 ;
;
 момент второй степени, а
момент второй степени, а
 момент первой степени, возведенный в
квадрат.
момент первой степени, возведенный в
квадрат.
Теоретически и практически доказано, что если при большом числе наблюдений к средней
арифметической прибавить и отнять от нее 1(М1), то в пределах полученных величин
будет находится 68,3% всех вариант вариационного ряда. Если к средней арифметической
прибавить и отнять 2(М2), то в пределах полученных величин будет находиться 95,5%
всех вариант. М 3включает в себя 99,7% всех вариант вариационного ряда.
Исходя из этого положения можно проверить типичность средней арифметической для
вариационного ряда, из которого она была вычислена. Для этого надо к средней
арифметической прибавить и от нее отнять утроенную (М3). Если в полученные пределы
данный вариационный ряд укладывается, то средняя арифметическая типична, т.е. она
выражает основную закономерность ряда и ей можно пользоваться.
Указанное положение широко применяется при выработке различных стандартов (одежды,
обуви, школьной мебели и т.д).
Степень разнообразия признака в вариационном ряду можно оценить покоэффициенту
вариации (отношение среднего квадратического отклонения к средней арифметической,
умноженное на 100%)
С v = х 100
При С v менее 10% отмечается слабое разнообразие, при С v 10-20% - среднее, а при более 20% -
сильное разнообразие признака.
Свойство 1. Средняя арифметическая постоянной величины равна этой постоянной: при
Свойство 2.
Алгебраическая сумма отклонений индивидуальных значений признака от средней арифметической равна нулю: ![]() для несгруппированных данных и
для несгруппированных данных и ![]() для рядов распределения.
для рядов распределения.
Это свойство означает, что сумма положительных отклонений равна сумме отрицательных отклонений, т.е. все отклонения, обусловленные случайными причинами взаимно погашаются.
Свойство 3.
Сумма квадратов отклонений индивидуальных значений признака от средней арифметической есть число минимальное: ![]() для несгруппировочных данных и
для несгруппировочных данных и ![]() для рядов распределения. Это свойство означает, что сумма квадратов отклонений индивидуальных значений признака от средней арифметической всегда меньше суммы отклонений вариантов признака от любого другого значения, даже мало отличающегося от средней.
для рядов распределения. Это свойство означает, что сумма квадратов отклонений индивидуальных значений признака от средней арифметической всегда меньше суммы отклонений вариантов признака от любого другого значения, даже мало отличающегося от средней.
Второе и третье свойство средней арифметической применяются для проверки правильности расчета средней величины; при изучении закономерностей изменения уровней ряда динамики; для нахождения параметров уравнения регрессии при изучении корреляционной связи между признаками.
Все три первых свойства выражают сущностные черты средней как статистической категории.
Следующие свойства средней рассматриваются как вычислительные, поскольку они имеют некоторое прикладное значение.
Свойство 4. Если все веса (частоты) разделить на какое-либо постоянное число d, то средняя арифметическая не изменится, поскольку это сокращение в равной степени коснется и числителя и знаменателя формулы расчета средней.
Из этого свойства вытекают два важных следствия.
Следствие 1. Если все веса равны между собой, то вычисление средней арифметической взвешенной можно заменить вычислением средней арифметической простой.
Следствие 2 . Абсолютные значения частот (весов) можно заменять их удельными весами.
Свойство 5. Если все варианты разделить или умножить на какое-либо постоянное число d, то средняя арифметическая уменьшиться или увеличиться в d раз.
Свойство 6. Если все варианты уменьшить или увеличить на постоянной число A, то и со средней произойдут аналогичные изменения.
Прикладные свойства средней арифметической можно проиллюстрировать, применив способ расчета средней от условного начала (способ моментов).
Средняя арифметическая способом моментов вычисляется по формуле:
где А – середина какого-либо интервала (предпочтение отдается центральному);
d – величина равновеликого интервала, или наибольший кратный делитель интервалов;
m 1 – момент первого порядка.
Момент первого порядка определяется следующим образом:
 .
.
Технику применения этого способа расчета проиллюстрируем по данным предшествующего примера.
Таблица 5.6
| Стаж работы, лет | Число рабочих | Середина интервала x | |||
| до 5 | 2,5 | -10 | -2 | -28 | |
| 5-10 | 7,5 | -5 | -1 | -22 | |
| 10-15 | 12,5 | ||||
| 15-20 | 17,5 | +5 | +1 | +25 | |
| 20 и выше | 22,5 | +10 | +2 | +22 | |
| Итого | Х | Х | Х | -3 |
Как видно из расчетов, приведенных в табл. 5.6 из всех вариантов вычитается одно из их значений 12,5, которое приравнивается нулю и служит условным началом отсчета. В результате деления разностей на величину интервала – 5 получают новые варианты.
Согласно итогу табл. 5.6 имеем: ![]() .
.
Результат вычислений по способу моментов аналогичен результату, который был получен применением основного способа расчета по средней арифметической взвешенной.
Структурные средние
В отличие от степенных средних, которые рассчитываются на основе использования всех вариант значений признака, структурные средние выступают как конкретные величины, совпадающие с вполне определенными вариантами ряда распределения. Мода и медиана характеризуют величину варианта, занимающего определенное положение в ранжированном вариационном ряду.
Мода – это величина признака, которая чаще всего встречается в данной совокупности. В вариационном ряду это будет варианта, имеющая наибольшую частоту.
Нахождение моды в дискретном ряду распределения не требует вычислений. Путем просмотра столбца частот находят наибольшую частоту.
Например, распределение рабочих предприятия по квалификации характеризуются данными табл. 5.7.
Таблица 5.7
Наибольшая частота в этом ряду распределения 80, значит мода равна четвертому разряду. Следовательно, наиболее часто встречаются рабочие, имеющие четвертый разряд.
Если ряд распределения интервальный , то по наибольшей частоте устанавливают только модальный интервал, а затем уже вычисляют моду по формуле:
![]() ,
,
где – нижняя граница модального интервала;
– величина модального интервала;
– частота модального интервала;
– частота предмодального интервала;
– частота послемодального интервала.
Вычислим моду по данным, приведенным в табл. 5.8.
Таблица 5.8
Это значит, что чаще всего предприятия имеют прибыль 726 млн р.
Практическое применение моды ограниченно. На значение моды ориентируются, когда определяют наиболее ходовые размеры обуви и одежды при планировании их производства и реализации, при изучении цен на оптовых и розничных рынках (метод основного массива). Моду используют вместо средней величины при подсчете возможных резервов производства.
Медиана соответствует варианте, стоящей в центре ранжированного ряда распределения. Это значение признака, которое делит всю совокупность на две равные части.
Положение медианы определяется ее номером (N).
где – число единиц совокупности. Используем данные примера, приведенные в табл. 5.7 для определения медианы.
![]() , т.е. медиана равна средней арифметической из 100-го и 110-го значений признака. По накопленным частотам определяем, что 100-я и 110-я единицы ряда имеют величину признака, равную четвертому разряду, т.е. медиана равна четвертому разряду.
, т.е. медиана равна средней арифметической из 100-го и 110-го значений признака. По накопленным частотам определяем, что 100-я и 110-я единицы ряда имеют величину признака, равную четвертому разряду, т.е. медиана равна четвертому разряду.
Медиана в интервальном ряду распределения определяется в следующем порядке.
1. Подсчитываются накопленные частоты по данному ранжированному ряду распределения.
2. На основе накопленных частот устанавливается медианный интервал. Он находится там, где первая накопленная частота равна или больше половины совокупности (всех частот).
3. Вычисляется медиана по формуле:
 ,
,
где – нижняя граница медианного интервала;
– величина интервала;
– сумма всех частот;
– сумма накопленных частот, предшествующих медианному интервалу;
– частота медианного интервала.
Вычислим медиану по данным табл. 5.8.
Первая накопленная частота, которая равна половине совокупности 30, значит медиана находится в интервале 500-700.
![]()
Это означает, что половина предприятий получает прибыль до 676 млн р., а другая половина свыше 676 млн р.
Медиану часто используют вместо средней величины, когда совокупность неоднородна, т.к. она не находится под влиянием крайних значений признака. Практическое применение медианы также связано с ее свойством минимальности. Абсолютная сумма отклонений индивидуальных значений от медианы есть величина наименьшая. Поэтому медиану применяют в расчетах при проектировании места расположения объектов, которые будут использоваться различными организациями и лицами.
ЦЕЛЬ ЗАНЯТИЯ: Овладеть основами вариационной статистики, навыками вычисления и оценки достоверности средних величин
МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЯ: Студенты самостоятельно готовятся к практическому занятию по рекомендованной литературе и выполняют индивидуальное домашнее задание. Преподаватель в течение 10 минут проверяет правильность выполнения домашнего задания и указывает на допущенные ошибки, проверяет степень подготовки с использованием тестирования и устного опроса. Затем студенты самостоятельно вычисляют средние величины и оценивают их достоверность. В конце занятия преподаватель проверяет самостоятельную работу студентов.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. Что представляет собой вариационный ряд, какие виды вариационных рядов выделяют в статистике, каковы элементы вариационного ряда.
2. Что такое средние величины, возможности их использования в медицине и практической деятельности врача.
3. Виды средних величин: мода, медиана, средняя арифметическая
4. Методика вычисления средней арифметической и параметров, характеризующих среднюю.
5. Какие математические законы позволяют теоретически обосновать достоверность статистических данных.
6. Как определить среднюю ошибку средней величины.
7. Что понимается под доверительной границей производных величин.
8. Оценка достоверности различий средних величин при помощи доверительного коэффициента t.
9. Оценка критерия достоверности при больших и малых выборках.
В медико-социальных исследованиях наряду с абсолютными и относительными широко используются средние величины. Средняя величина – это совокупная обобщающая характеристика количественных признаков, она обычно обозначается буквой М или Х. Средние величины существенно отличаются от статистических коэффициентов:
1. Коэффициенты характеризуют признак, встречающийся только у некоторой части статистического коллектива, так называемый альтернативный признак, который может иметь место или не иметь место (рождение, смерть, заболевание, инвалидность).
Средние величины охватывают признаки, присущие всем членам коллектива, но в разной степени (вес, рост, дни лечения в больнице).
2. Коэффициенты применяются для измерения качественных признаков. Средние величины - для варьирующих количественных признаков.
Применение средних величин в медико-социальных исследованиях широко используется при изучении физического развития. Кроме того, средние величины применяются:
1. Для характеристики организации работы лечебно-профилактических учреждений и оценки их деятельности:
А) в поликлинике: показатели нагрузки врачей, посещаемость поликлиники, среднее число посещений на 1-м году жизни, среднее число детей на участке, среднее число посещений при определенном заболевании и т. д.;
Б) в стационаре: среднее число дней работы койки в году; средняя длительность лечения при определенных заболеваниях и т. д.;
В) в органах санэпиднадзора: средняя площадь (или кубатура) на 1 человека, средние нормы питания (белки, жиры, углеводы, витамины, минеральные соли, калории) в дневном рационе возрастных групп у детей и взрослых и т. д.
2. Для определения медико-физиологических показателей организма в норме и патологии в клинических и экспериментальных исследованиях.
3. В специальных демографических и медико-социальных исследованиях.
Для расчета средней величины необходимо построить вариационный ряд - т. е. ряд числовых измерений определенного признака, отличающихся по своей величине.
Вариационные ряды бывают следующих видов:
А) ранжированный, неранжированный;
Б) сгруппированный, несгруппированный;
В) прерывный, непрерывный.
Ранжированный ряд - упорядоченный ряд; варианты располагаются последовательно по нарастанию или убыванию числовых значений.
Неранжированный ряд - варианты располагаются бессистемно.
Прерывный (дискретный) ряд - варианты выражены в виде целых (дискретных) чисел (окна в избе).
Непрерывный ряд – варианты могут быть выражены дробными числами.
Несгруппированный ряд – каждому значению варианты соответствует определенное число частот.
Сгруппированный ряд (интервальный) – варианты соединены в группы, объединяющие их по величине в пределах определенного интервала.
В статистике принято выделять следующие виды средних величин: мода (Мо), медиана (Ме) и средняя арифметическая (М). Мода – величина варьирующего признака, наиболее часто встречающаяся в совокупности. В вариационном ряду это варианта, имеющая наибольшую частоту встречаемости. Обычно мода является величиной довольно близкой к средней арифметической, совпадает с ней при полной симметрии распределения. Медиана – варианта, делящая вариационный ряд на две равные половины. При нечетном числе наблюдений медианой является варианта, имеющая в вариационном ряду порядковый номер (n + 1): 2. Средняя арифметическая величина (М) – в отличие от моды и медианы опирается на все произведенные наблюдения, поэтому является важной характеристикой для всего распределения.
В зависимости от вида вариационного ряда используется тот или иной способ расчета средней. Средняя арифметическая для простого ряда, где каждая варианта встречается один раз, вычисляется по формуле: М =
Знак суммы, V –отдельные значения вариант, n –число наблюдений. Средняя арифметическая взвешенная определяется по формуле: М=
Знак суммы, V –отдельные значения вариант, n –число наблюдений, р – частота встречаемости вариант. Одним из наиболее простых и достаточно точных способов расчета средней арифметической является способ моментов, основанный на том, что алгебраическая сумма отклонений каждой варианты вариационного ряда от средней арифметической равна нулю. М= А + i
Где А – условно принятая средняя или мода, а- отклонение каждой варианты от условно принятой средней, р –частота встречаемости вариант, n –число наблюдений, i – интервал или расстояние между соседними вариантами. Основные свойства средней величины: 1) имеет абстрактный характер, так как является обобщающей величиной: в ней стираются случайные колебания; 2) занимает срединное положение в ряду (в строго симметричном ряду); 3) сумма отклонений всех вариант от средней величины равна нулю. Данное свойство средней величины используется для проверки правильности расчета средней. Она оценивается по уровню колеблемости вариационного ряда. Критериями такой оценки могут служить: амплитуда (разница между крайними вариантами); среднее квадратическое отклонение, показывающее, как отличаются варианты от рассчитанной средней величины; коэффициент вариации.
Среднеквадратическое отклонение (
) наиболее точно характеризует степень разнообразия варьирующего признака, без чего нельзя достаточно полно охарактеризовать явление. Для простого вариационного ряда (р =1) среднеквадратическое отклонение расчитывается по формуле
Для взвешенного вариационного ряда по формуле:
Где d = V – M - отклонение каждой варианты от средней арифметической. При числе наблюдений меньше 30 в знаменателе этих формул берется не n, а n – 1 (так называемое в статистике число степеней свободы). При числе наблюдений более 30 уменьшение знаменателя на единицу не имеет практического значения, т.к. существенно не сказывается на конечном результате. Значительно упрощает вычисления расчет среднего квадратического отклонения по способу моментов.

где, величина
называется моментом первой степени, а
Моментом второй степени.
Степень разнообразия (колеблемости) признака в вариационном ряду можно оценить по коэффициенту вариации (отношение среднего квадратического отклонения к средней величине, умноженное на 100%); при вариации менее 10% отмечается слабое разнообразие, при вариации 10-20% - среднее, а при вариации более 20% - сильное разнообразие признака. Если нет возможности сравнить вариационный ряд с другими, то используют правило трех сигм. Если к средней прибавить одну сигму, то этой вычисленной средней соответствует 68,3%, при двух сигмах - 95,4%, при трех сигмах - 99,7% от всех признаков. В медицине с величиной М ± 1? связано понятие нормы; отклонения от средней (в любую сторону) больше, чем на 1?, но меньше чем на 2?, считаются субнормальными (выше или ниже нормы), а при отклонении от средней больше чем на 2?, варианты считаются значительно отличающимися от нормы (патология).
Мерой точности и достоверности результатов выборочных статистических величин являются средние ошибки представительности (репрезентативности). Средняя ошибка средней арифметической – m (отношение среднего квадратического отклонения к квадратному корню из общего числа наблюдений - объектов). m =
Мерой достоверности среднего показателя наряду с его ошибкой являются, доверительные границы и достоверность разности между двумя средними величинами.
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ:
ЗАДАНИЕ №1. Определить моду и медиану вариационного ряда. На основе приведенных данных вычислите: среднюю арифметическую по способу моментов, среднее квадратическое отклонение, коэффициент вариации, среднюю ошибку средней арифметической
Задача 1.
Вычислите среднюю длительность пребывания больного в хирургическом отделении стационара
Задача 2.
Вычислите среднюю длительность временной нетрудоспособности при гипертонической болезни II стадии (гипертонический криз)
Вычислите среднюю частоту пульса в группе здоровых мужчин в возрасте 22 года после умеренной физической нагрузки
Задача 4.
Вычислите среднюю жилую площадь, приходящуюся на одного человека в семьях с низким уровнем достатка
Задача 5.
Вычислите средний вес у девочек 12 лет, воспитывающихся в интернате
Задача 6.
Вычислите максимальную мышечную силу правой кисти у 15-летних юношей, регулярно посещающих спортивные секции
Задача 7.
Вычислите средний рост 17-летних девушек, обучающихся в общеобразовательной школе.
Задача 8.
Вычислите среднее число пациентов принятых участковым терапевтом за один рабочий день

Задача 9.
Вычислите среднее число детей в дагестанской семье
Задача 10.
Вычислите среднее число пораженных кариесом зубов у 18 летних студенток медицинской академии (индекс КПУ)
Задача 11.
Вычислите среднее число детей первого года жизни, проживающих на одном педиатрическом участке
Задача 12.
Вычислить среднее число пропущенных занятий по дисциплине «Общественное здоровье и здравоохранение» студентами 4 курса лечебного факультета в весеннем семестре
Задача 13.
Вычислите средний рост призывников в Ставропольском крае
Задача 14.
Вычислите среднее число пациентов принятых хирургом в поликлинике за один рабочий день

ЗАДАНИЕ №2. Для средних величин, вычисленных в предыдущем задании определите доверительные границы с вероятностью безошибочного прогноза 95%.
Ю.П. Лисицын. Общественное здоровье и здравоохранение. Учебник для вузов. М., 2002.
Ю.П. Лисицын. Социальная гигиена (медицина) и организация здравоохранения. Казань, 1999. –с. 288-289.
В.К. Юрьев, Г.И. Куценко. Общественное здоровье и здравоохранение. С.-П., 2000. –с. 191-199.
А.Ф. Серенко, В.В. Ермаков. Социальная гигиена и организация здравоохранения. М., 1984. –с.124-146.
Общественное здоровье и здравоохранение. Под ред. В.А. Миняева, Н.И. Вишнякова. М. «МЕДпресс-информ», 2002. –с. 97-107.
Руководство по социальной гигиене и организации здравоохранения. Под ред. Ю.П. Лисицына. М., 1987.
Зайцев В.М., Лифляндский В.Г., Маринкин В.И. Прикладная медицинская статистика. С.-П. «Фолиант», 2003.

 кг.
кг. 10 слов с ударением на 1 слог
10 слов с ударением на 1 слог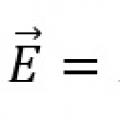 Закон Ома для замкнутой цепи и неоднородного участка цепи
Закон Ома для замкнутой цепи и неоднородного участка цепи Чиновники-академики уволены с госслужбы
Чиновники-академики уволены с госслужбы