Преобразование выражений с дробными степенями. Преобразование выражений. Подробная теория (2020). Преобразование выражений с корнями и степенями
Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.
Что представляют собой степенные выражения?
В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.
Определение 1
Степенное выражение – это выражение, которое содержит степени.
Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.
Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 3 2 , 7 5 + 1 , (2 + 1) 5 , (− 0 , 1) 4 , 2 2 3 3 , 3 · a 2 − a + a 2 , x 3 − 1 , (a 2) 3 . А также степени с нулевым показателем: 5 0 , (a + 1) 0 , 3 + 5 2 − 3 , 2 0 . И степени с целыми отрицательными степенями: (0 , 5) 2 + (0 , 5) - 2 2 .
Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 264 1 4 - 3 · 3 · 3 1 2 , 2 3 , 5 · 2 - 2 2 - 1 , 5 , 1 a 1 4 · a 1 2 - 2 · a - 1 6 · b 1 2 , x π · x 1 - π , 2 3 3 + 5 .
В качестве показателя может выступать переменная 3 x - 54 - 7 · 3 x - 58 или логарифм x 2 · l g x − 5 · x l g x .
С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.
Основные виды преобразований степенных выражений
В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.
Пример 1
Вычислите значение степенного выражения 2 3 · (4 2 − 12) .
Решение
Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 2 3 · (4 2 − 12) = 2 3 · (16 − 12) = 2 3 · 4 .
Нам остается заменить степень 2 3 ее значением 8 и вычислить произведение 8 · 4 = 32 . Вот наш ответ.
Ответ: 2 3 · (4 2 − 12) = 32 .
Пример 2
Упростите выражение со степенями 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 .
Решение
Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .
Ответ: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .
Пример 3
Представьте выражение со степенями 9 - b 3 · π - 1 2 в виде произведения.
Решение
Представим число 9 как степень 3 2 и применим формулу сокращенного умножения:
9 - b 3 · π - 1 2 = 3 2 - b 3 · π - 1 2 = = 3 - b 3 · π - 1 3 + b 3 · π - 1
Ответ: 9 - b 3 · π - 1 2 = 3 - b 3 · π - 1 3 + b 3 · π - 1 .
А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.
Работа с основанием и показателем степени
Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, (2 + 0 , 3 · 7) 5 − 3 , 7 и . Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.
Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.
Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, (2 + 0 , 3 · 7) 5 − 3 , 7 можно выполнить действия для перехода к степени 4 , 1 1 , 3 . Раскрыв скобки, мы можем привести подобные слагаемые в основании степени (a · (a + 1) − a 2) 2 · (x + 1) и получить степенное выражение более простого вида a 2 · (x + 1) .
Использование свойств степеней
Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s - произвольные действительные числа:
Определение 2
- a r · a s = a r + s ;
- a r: a s = a r − s ;
- (a · b) r = a r · b r ;
- (a: b) r = a r: b r ;
- (a r) s = a r · s .
В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство a m · a n = a m + n , где m и n – натуральные числа, то оно будет верно для любых значений a , как положительных, так и отрицательных, а также для a = 0 .
Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.
При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».
Пример 4
Представьте выражение a 2 , 5 · (a 2) − 3: a − 5 , 5 в виде степени с основанием a .
Решение
Для начала используем свойство возведения в степень и преобразуем по нему второй множитель (a 2) − 3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:
a 2 , 5 · a − 6: a − 5 , 5 = a 2 , 5 − 6: a − 5 , 5 = a − 3 , 5: a − 5 , 5 = a − 3 , 5 − (− 5 , 5) = a 2 .
Ответ: a 2 , 5 · (a 2) − 3: a − 5 , 5 = a 2 .
Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.
Пример 5
Найти значение степенного выражения 3 1 3 · 7 1 3 · 21 2 3 .
Решение
Если мы применим равенство (a · b) r = a r · b r , справа налево, то получим произведение вида 3 · 7 1 3 · 21 2 3 и дальше 21 1 3 · 21 2 3 . Сложим показатели при умножении степеней с одинаковыми основаниями: 21 1 3 · 21 2 3 = 21 1 3 + 2 3 = 21 1 = 21 .
Есть еще один способ провести преобразования:
3 1 3 · 7 1 3 · 21 2 3 = 3 1 3 · 7 1 3 · (3 · 7) 2 3 = 3 1 3 · 7 1 3 · 3 2 3 · 7 2 3 = = 3 1 3 · 3 2 3 · 7 1 3 · 7 2 3 = 3 1 3 + 2 3 · 7 1 3 + 2 3 = 3 1 · 7 1 = 21
Ответ: 3 1 3 · 7 1 3 · 21 2 3 = 3 1 · 7 1 = 21
Пример 6
Дано степенное выражение a 1 , 5 − a 0 , 5 − 6 , введите новую переменную t = a 0 , 5 .
Решение
Представим степень a 1 , 5 как a 0 , 5 · 3 . Используем свойство степени в степени (a r) s = a r · s справа налево и получим (a 0 , 5) 3: a 1 , 5 − a 0 , 5 − 6 = (a 0 , 5) 3 − a 0 , 5 − 6 . В полученное выражение можно без проблем вводить новую переменную t = a 0 , 5 : получаем t 3 − t − 6 .
Ответ: t 3 − t − 6 .
Преобразование дробей, содержащих степени
Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.
Пример 7
Упростить степенное выражение 3 · 5 2 3 · 5 1 3 - 5 - 2 3 1 + 2 · x 2 - 3 - 3 · x 2 .
Решение
Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:
3 · 5 2 3 · 5 1 3 - 5 - 2 3 1 + 2 · x 2 - 3 - 3 · x 2 = 3 · 5 2 3 · 5 1 3 - 3 · 5 2 3 · 5 - 2 3 - 2 - x 2 = = 3 · 5 2 3 + 1 3 - 3 · 5 2 3 + - 2 3 - 2 - x 2 = 3 · 5 1 - 3 · 5 0 - 2 - x 2
Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12 - 2 - x 2 = - 12 2 + x 2
Ответ: 3 · 5 2 3 · 5 1 3 - 5 - 2 3 1 + 2 · x 2 - 3 - 3 · x 2 = - 12 2 + x 2
Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Пример 8
Приведите дроби к новому знаменателю: а) a + 1 a 0 , 7 к знаменателю a , б) 1 x 2 3 - 2 · x 1 3 · y 1 6 + 4 · y 1 3 к знаменателю x + 8 · y 1 2 .
Решение
а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a 0 , 7 · a 0 , 3 = a 0 , 7 + 0 , 3 = a , следовательно, в качестве дополнительного множителя мы возьмем a 0 , 3 . Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a 0 , 3 не обращается в нуль.
Выполним умножение числителя и знаменателя дроби на a 0 , 3 :
a + 1 a 0 , 7 = a + 1 · a 0 , 3 a 0 , 7 · a 0 , 3 = a + 1 · a 0 , 3 a
б) Обратим внимание на знаменатель:
x 2 3 - 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 2 - x 1 3 · 2 · y 1 6 + 2 · y 1 6 2
Умножим это выражение на x 1 3 + 2 · y 1 6 , получим сумму кубов x 1 3 и 2 · y 1 6 , т.е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь.
Так мы нашли дополнительный множитель x 1 3 + 2 · y 1 6 . На области допустимых значений переменных x
и y
выражение x 1 3 + 2 · y 1 6 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1 x 2 3 - 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 + 2 · y 1 6 x 2 3 - 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 3 + 2 · y 1 6 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2
Ответ: а) a + 1 a 0 , 7 = a + 1 · a 0 , 3 a , б) 1 x 2 3 - 2 · x 1 3 · y 1 6 + 4 · y 1 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2 .
Пример 9
Сократите дробь: а) 30 · x 3 · (x 0 , 5 + 1) · x + 2 · x 1 1 3 - 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 - 5 3 , б) a 1 4 - b 1 4 a 1 2 - b 1 2 .
Решение
а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15 . Также мы можем произвести сокращение на x 0 , 5 + 1 и на x + 2 · x 1 1 3 - 5 3 .
Получаем:
30 · x 3 · (x 0 , 5 + 1) · x + 2 · x 1 1 3 - 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 - 5 3 = 2 · x 3 3 · (x 0 , 5 + 1)
б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:
a 1 4 - b 1 4 a 1 2 - b 1 2 = a 1 4 - b 1 4 a 1 4 2 - b 1 2 2 = = a 1 4 - b 1 4 a 1 4 + b 1 4 · a 1 4 - b 1 4 = 1 a 1 4 + b 1 4
Ответ: а) 30 · x 3 · (x 0 , 5 + 1) · x + 2 · x 1 1 3 - 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 - 5 3 = 2 · x 3 3 · (x 0 , 5 + 1) , б) a 1 4 - b 1 4 a 1 2 - b 1 2 = 1 a 1 4 + b 1 4 .
К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
Пример 10
Выполните действия x 1 2 + 1 x 1 2 - 1 - x 1 2 - 1 x 1 2 + 1 · 1 x 1 2 .
Решение
Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:
x 1 2 - 1 · x 1 2 + 1
Вычтем числители:
x 1 2 + 1 x 1 2 - 1 - x 1 2 - 1 x 1 2 + 1 · 1 x 1 2 = = x 1 2 + 1 · x 1 2 + 1 x 1 2 - 1 · x 1 2 + 1 - x 1 2 - 1 · x 1 2 - 1 x 1 2 + 1 · x 1 2 - 1 · 1 x 1 2 = = x 1 2 + 1 2 - x 1 2 - 1 2 x 1 2 - 1 · x 1 2 + 1 · 1 x 1 2 = = x 1 2 2 + 2 · x 1 2 + 1 - x 1 2 2 - 2 · x 1 2 + 1 x 1 2 - 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 - 1 · x 1 2 + 1 · 1 x 1 2
Теперь умножаем дроби:
4 · x 1 2 x 1 2 - 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 - 1 · x 1 2 + 1 · x 1 2
Произведем сокращение на степень x 1 2 , получим 4 x 1 2 - 1 · x 1 2 + 1 .
Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4 x 1 2 - 1 · x 1 2 + 1 = 4 x 1 2 2 - 1 2 = 4 x - 1 .
Ответ: x 1 2 + 1 x 1 2 - 1 - x 1 2 - 1 x 1 2 + 1 · 1 x 1 2 = 4 x - 1
Пример 11
Упростите степенное выражение x 3 4 · x 2 , 7 + 1 2 x - 5 8 · x 2 , 7 + 1 3 .
Решение
Мы можем произвести сокращение дроби на (x 2 , 7 + 1) 2 . Получаем дробь x 3 4 x - 5 8 · x 2 , 7 + 1 .
Продолжим преобразования степеней икса x 3 4 x - 5 8 · 1 x 2 , 7 + 1 . Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x 3 4 x - 5 8 · 1 x 2 , 7 + 1 = x 3 4 - - 5 8 · 1 x 2 , 7 + 1 = x 1 1 8 · 1 x 2 , 7 + 1 .
Переходим от последнего произведения к дроби x 1 3 8 x 2 , 7 + 1 .
Ответ: x 3 4 · x 2 , 7 + 1 2 x - 5 8 · x 2 , 7 + 1 3 = x 1 3 8 x 2 , 7 + 1 .
Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x + 1) - 0 , 2 3 · x - 1 можно заменить на x 3 · (x + 1) 0 , 2 .
Преобразование выражений с корнями и степенями
В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.
Пример 12
Представьте выражение x 1 9 · x · x 3 6 в виде степени.
Решение
Область допустимых значений переменной x определяется двумя неравенствами x ≥ 0 и x · x 3 ≥ 0 , которые задают множество [ 0 , + ∞) .
На этом множестве мы имеем право перейти от корней к степеням:
x 1 9 · x · x 3 6 = x 1 9 · x · x 1 3 1 6
Используя свойства степеней, упростим полученное степенное выражение.
x 1 9 · x · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 · 1 3 · 6 = = x 1 9 · x 1 6 · x 1 18 = x 1 9 + 1 6 + 1 18 = x 1 3
Ответ: x 1 9 · x · x 3 6 = x 1 3 .
Преобразование степеней с переменными в показателе
Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 5 2 · x + 1 − 3 · 5 x · 7 x − 14 · 7 2 · x − 1 = 0 .
Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:
5 2 · x · 5 1 − 3 · 5 x · 7 x − 14 · 7 2 · x · 7 − 1 = 0 , 5 · 5 2 · x − 3 · 5 x · 7 x − 2 · 7 2 · x = 0 .
Теперь поделим обе части равенства на 7 2 · x . Это выражение на ОДЗ переменной x принимает только положительные значения:
5 · 5 - 3 · 5 x · 7 x - 2 · 7 2 · x 7 2 · x = 0 7 2 · x , 5 · 5 2 · x 7 2 · x - 3 · 5 x · 7 x 7 2 · x - 2 · 7 2 · x 7 2 · x = 0 , 5 · 5 2 · x 7 2 · x - 3 · 5 x · 7 x 7 x · 7 x - 2 · 7 2 · x 7 2 · x = 0
Сократим дроби со степенями, получим: 5 · 5 2 · x 7 2 · x - 3 · 5 x 7 x - 2 = 0 .
Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5 · 5 7 2 · x - 3 · 5 7 x - 2 = 0 , которое равносильно 5 · 5 7 x 2 - 3 · 5 7 x - 2 = 0 .
Введем новую переменную t = 5 7 x , что сводит решение исходного показательного уравнения к решению квадратного уравнения 5 · t 2 − 3 · t − 2 = 0 .
Преобразование выражений со степенями и логарифмами
Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 1 4 1 - 5 · log 2 3 или log 3 27 9 + 5 (1 - log 3 5) · log 5 3 . Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Выражением вида a (m/n) , где n - некоторое натуральное число, m - некоторое целое число и основание степени а больше нуля, называется степень с дробным показателем. Причем верным является следующее равенство. n√(a m) = a (m/n) .
Как мы уже знаем, числа вида m/n, где n - некоторое натуральное число, а m - некоторое целое число, называют дробными или рациональными числами. Из всего вышесказанного получаем, что степень определена, для любого рационального показателя степени и любого положительного основания степени.
Для любых рациональных чисел p,q и любых a>0 и b>0 верны следующие равенства:
- 1. (a p)*(a q) = a (p+q)
- 2. (a p):(b q) = a (p-q)
- 3. (a p) q = a (p*q)
- 4. (a*b) p = (a p)*(b p)
- 5. (a/b) p = (a p)/(b p)
Данные свойства широко используются при преобразовании различных выражений, где содержатся степени с дробными показателями.
Примеры преобразований выражений, содержащих степень с дробным показателем
Рассмотрим несколько примеров, демонстрирующих применение этих свойств для преобразования выражений.
1. Вычислить 7 (1/4) * 7 (3/4) .
- 7 (1/4) * 7 (3/4) = z (1/4 + 3/4) = 7.
2. Вычислить 9 (2/3) : 9 (1/6) .
- 9 (2/3) : 9 (1/6) = 9 (2/3 - 1/6) = 9 (1/2) = √9 = 3.
3. Вычислить (16 (1/3)) (9/4) .
- (16 (1/3)) (9/4) = 16 ((1/3)*(9/4)) =16 (3/4) = (2 4) (3/4) = 2 (4*3/4) = 2 3 = 8.
4. Вычислить 24 (2/3) .
- 24 (2/3) = ((2 3)*3) (2/3) = (2 (2*2/3))*3 (2/3) = 4*3√(3 2)=4*3√9.
5. Вычислить (8/27) (1/3) .
- (8/27) (1/3) = (8 (1/3))/(27 (1/3)) = ((2 3) (1/3))/((3 3) (1/3))= 2/3.
6. Упростить выражение ((a (4/3))*b + a*b (4/3))/(3√a + 3√b)
- ((a (4/3))*b + a*b (4/3))/(3√a + 3√b) = (a*b*(a (1/3) + b (1/3)))/(1/3) + b (1/3)) = a*b.
7. Вычислить (25 (1/5))*(125 (1/5)).
- (25 (1/5))*(125 (1/5)) =(25*125) (1/5) = (5 5) (1/5) = 5.
8. Упростить выражение
- (a (1/3) - a (7/3))/(a (1/3) - a (4/3)) - (a (-1/3) - a (5/3))/(a (2/3) + a (-1/3)).
- (a (1/3) - a (7/3))/(a (1/3) - a (4/3)) - (a (-1/3) - a (5/3))/(a (2/3) + a (-1/3)) =
- = ((a (1/3))*(1-a 2))/((a (1/3))*(1-a)) - ((a (-1/3))*(1-a 2))/ ((a (-1/3))*(1+a)) =
- = 1 +a - (1-a) = 2*a.
Как видите используя эти свойства, можно значительно упростить некоторые выражения, которые содержат степени с дробными показателями.
Муниципальное казённое общеобразовательное учреждение
основная общеобразовательная школа № 25
Урок алгебры
Тема:
« Преобразование выражений, содержащих степени с дробными показателями»
Разработала:
,
учитель математики
высшей к валификационной категории
Узловая
2013
Тема урока : Преобразование выражений, содержащих степени с дробными показателями
Цель урока :
1. Дальнейшее формирование умений, знаний, навыков преобразования выражений, содержащих степени с дробными показателями
2. Развитие умения находить ошибки, развитие мышления, творчества, речи, вычислительных навыков
3. Воспитание самостоятельности, интереса к предмету, внимательности, аккуратности.
ТСО: магнитная доска, контрольные карточки, таблицы, индивидуальные карточки, у школьников на столе чистые подписанные листы для индивидуальной работы, кроссворд, таблицы для математической разминки, мультимедийный проектор.
Тип урока : закрепление ЗУН.
План урока во времени
1. Организационные моменты (2 мин)
2. Проверка домашнего задания (5 мин)
3. Разгадывание кроссворда (3 мин)
4. Математическая разминка (5 мин)
5. Решение упражнений на закрепление фронтально (7 мин)
6. Индивидуальные работы (10 мин)
7. Решение упражнений на повторение (5 мин)
8. Итог урока (2 мин)
9. Задание на дом (1 мин)
Ход урока
1) Проверка домашнего задания в форме взаимопроверки . Хорошие ученики проверяют тетради у слабых ребят. А слабые ребята проверяют у сильных по образцу контрольной карточки. Домашнее задание дано в двух вариантах.
I вариант задание нетрудное
II вариант задание сложное
В результате проверки ребята подчёркивают ошибки простым карандашом и ставят оценку. Окончательно я проверяю работы, после того, как ребята сдадут тетради после урока. Я спрашиваю у ребят результаты их проверки и выставляю оценки за этот вид работы в свою таблицу подведения итогов.
2) Для проверки теоретического материала предлагается кроссворд .
По вертикали:
1. Свойство умножения, используемое при умножении одночлена на многочлен?
2. Действие показателей степени при возведении степени в степень?
3. Степень с нулевым показателем?
4. Произведение, состоящее из одинаковых множителей?
По горизонтали:
5. Корень n – ой степени из неотрицательного числа?
6. Действие показателей при умножении степеней?
7. Действие показателей степени при делении степеней?
8. Число всех одинаковых множителей?
3) Математическая разминка
а) выполните вычисление и с помощью шифра прочтите запрятанное в задачу слово.
На доске перед вами таблица. В таблице в графе 1 записаны примеры, которые надо вычислить.
Ключ к таблице
491/2 | ||
27-1/3 | ||
4*81/3 | ||
5*25-1/2 | ||
7*82/3 | ||
(49/144)1/2 | 7/12 | |
(27*64)1/3 |
7/12 |
А ответ записать в графе II , а в графе III поставить букву, соответствующую этому ответу.
Учитель: Итак, зашифрованное слово «степень». В следующем задании мы работаем со 2-й и 3-ей степенью
б) Игра «Смотри не ошибись»
Вместо точек поставьте число
а) х=(х…)2; б) а3/2 = (а1/2)…; в) а=(а1/3)…; г) 5… = (51/4)2; д) 34/3=(34/9)…; е) 74/5 = (7…)2; ж) х1/2=(х…)2; з) у1/2=(у…)2
Найдём ошибку:
А1/4 – 2а1/2 + 1 = (а1/
Итак, ребята, что же нужно было применить, для выполнения этого задания:
Свойство степеней: при возведении степени в степень показатели перемножаются;
4) А теперь приступаем к фронтальной письменной работе , используя результаты предыдущей работы. Открывают тетради записывают число, тему урока.
№ 000
а) а – в = (а1/2)2 – (в1/2)2 = (а1/2 – в1/2)*(а1/2 + в1/2)
б) а – в = (а1/3)3 – (в1/3)3 = (а1/3 – в1/3)*(а2/3 + а1/3 в1/3 + в2/3)
№ 000 (а, в, г, д)
а) m2 – 5 = m2 – (m1/2)2 = (m – 51/2)*(m+51/2)
в) a3 – 4 = (a3/2)2 – 22 = (a3/2 – 2)*(a3/2 +2)
г) x2/5 – y4/5 = (x1/5)2 – (y2/5)2 = (x1/5 – y2/5)*(x1/5 + y2/5)
д) 4 – a = 22 – (a1/2)2 = (2 – a1/2)*(2+a1/2)
№ 000 (а, г, е)
а) x3 – 2 = x3 – (21/3)3 = (x – 21/3)*(x2 + 21/3 x + 22/3)
г) a6/5 + 27 = (a2/5)3 + 33 = (a2/5 + 3)*(a4/3 – 3 a2/5 + 9)
е) 4 + y = (41/3)3 + (y1/3)3 = (41/3 + y1/3)*(42/3 + 41/3 y1/3 + y2/3)
Оценка
5) Работа по индивидуальным карточкам по четырём вариантам на отдельных листах
Задания с различной степенью сложности, выполняются без какой-либо подсказки учителя.
Проверяю работы сразу и ставлю оценки в свою таблицу и на листиках у ребят.
№ 000 (а, в, д, з)
а) 4*31/2/(31/2 – 3) = 4*31/2 /31/2*(1 – 31/2) = 4 / (1 – 31/2)
в) х + х1/2 /2х = х1/2*(х1/2+1)/ 2*(х1/2)2 = (х1/2+1)/ 2х1/2
д) (а2/3 – в2/3)/(а1/3 +в1/3) = (а1/3)2 – (в1/3)2/(а1/3 +в1/3) = (а1/3 + в1/3)*(а1/3 –в1/3)/(а1/3 + в1/3) = а1/3 – в1/3
з) (х2/3 - х1/3 у1/3 +у2/3)/(х +у) = ((х1/3)2 – х1/3 у1/3 + (у1/3)2)/((х1/3)3 +(у1/3)3) = ((х1/3)2 – х1/3 у1/3 +(у1/3)2)/(х1/3 +у1/3)*((х1/3)2 – х1/3 у1/3 + (у1/3)2) = 1/ (х1/3 +у1/3)
7) Работа по индивидуальным карточкам с различной степенью сложности . В некоторых упражнениях есть рекомендации учителя, так как материал усложнён и слабым ребятам трудно справляться с работой
Так же предлагается четыре варианта. Оценивание происходит сразу. Я заношу все оценки в таблицу.
Задача № из сборника
Учитель задаёт вопросы:
1. Что надо найти в задаче?
2. Что для этого нужно знать?
3. Как выразить время 1 пешехода и 2 пешехода?
4. Сравнить время 1 и 2 пешехода по условию задачи и составить уравнение.
Решение задачи:
Пусть х (км/ч) – скорость 1 пешехода
Х +1 (км/ч) – скорость 2 пешехода
4/х (ч) – время пешехода
4/(х +1) (ч) – время второго пешехода
По условию задачи 4/х >4/ (х +1) на 12 мин
12 мин = 12 /60 ч = 1/5 ч
Составляем уравнение
Х/4 – 4/ (х +1) = 1/5
НОЗ: 5х(х +1) ≠ 0
5*4*(х+1) – 5*4х = х*(х+1)
20х + 20 – 20х – х2 – х = 0
Х2 +х –20 = 0
Д=1 – 4*(-20) = 81, 81>0, 2 к
х1 = (-1 -√81)/(-2) = 5 км/ч – скорость 1 пешехода
х2 = (-1 + √81)/(-2) = 4 – не подходит по смыслу задачи, так как х>0
Ответ: 5 км/ч – скорость 2 пешехода
9) Итог урока : Итак, ребята, сегодня на уроке мы закрепили знания, умения, навыки преобразования выражений, содержащих степени, применяли формулы сокращённого умножения, вынос общего множителя за скобки, повторили пройденный материал. Указываю на достоинства и недостатки.
Подведение итогов урока в таблице.
Кроссворд | Мат. разминка | Фронт. работа | Инд. работа К-1 | Инд. работа К-2 | ||||
10)Объявляю оценки. Задание на дом
Индивидуальные карточки К – 1 и К – 2
Меняю В – 1 и В – 2 ; В – 3 и В – 4, так как они равносильные
Приложения к уроку.
1) Карточки для домашнего задания
1. упростите
а) (х1/2 – у1/2)2 + 2х1/2 у1/2
б) (а3/2 + 5а1\2)2 – 10а2
2. представьте в виде суммы
а) а1/3 с1\4*(в2/3 + с3/4)
б) (а1/2 – в1/2)*(а + а1/2 в1\2 + в)
3. вынесите общий множитель
в) 151/3 +201/3
1. упростите
а) √m + √n – (m1/4 – n1/4)2
б) (а1/4 +в1/4)*(а1/8 + в1/8)*(а1\8 – в1/8)
2. представьте в виде суммы
а) х0,5 у0,5*(х-0,5 – у1,5)
б) (х1/3 +у1/3)*(х2\3 – х1/3 у1\3 +у2/3)
3. Вынесите общий множитель за скобки
б) в1\3 – в
в) (2а)1/3 – (5а)1\3
2) контрольная карточка для В – 2
а) √m + √n – (m 1|4 – n 1|4)2 = m 1|2 + n 1|2 – ((m 1|2)2 – 2 m 1/4 n 1/4 + (n 1/2)2) = m 1/2 + n 1/2 – m 1/2 + 2 m 1/4 n 1/4 – n 1/2 = 2 m 1/4 n 1/4
б) (а1/4 + в1/4)*(а1/8 + в1/8)*(а1/8 – в1/8) = (а1/4 + в1/4)*(а1/8)2 – (в1/8)2 = (а1/4 + в1/4)*(а1/4 – в1/4) = (а1/4)2 – (в1/4)2 = а1/2 – в1/2
а) х0,5 у0,5* (х-0,5- у1,5) = х0,5 у0,5 х-0,5 – х0,5 у0,5у1,5 = х0 у0,5 – х0,5 у2 = у0,5 – х0,5 у2
б) (х1/3 + у1/3)*(х2/3 – х1/3 у1\3 + у2/3) = (х1\3 + у1/3)*((х1/3)2 – х1/3 у1\3 + (у1/3)2) = (х1/3)2 + (у1/3)2 = х +у
а) 3 – 31/2 = 31/2 * (31/2 - 1)
б) в1/3 – в = в1/3 *(1 – в2/3)
в) (2а)1/3 – (5а)1/3 = а1/3*(21/3 – 51/3)
3) Карточки для первой индивидуальной работы
а) а – у, х ≥ 0, у ≥ 0
б) а – и, а ≥ 0
1. Разложите на множители представив в виде разности квадратов
а) а1/2 – в1/2
2. Разложите на множители представив в виде разности или суммы кубов
а) c1/3 + d1/3
1. Разложите на множители представив в виде разности квадратов
а) Х1/2 + У1/2
б) Х1/4 – У1/4
2. Разложите на множители представив в виде разности или суммы кубов
4) карточки для второй индивидуальной работы
а) (х – х1/2)/ (х1/2 – 1)
Указание: х1/2 вынести за скобку числители
б) (а - в)/(а1/2 – в1/2)
Указание: а – в = (а1/2)2 – (в1/2)2
Сократите дробь
а) (21/4 – 2)/ 5*21/4
Указание: 21/4 вынести за скобку
б) (а – в)/(5а1/2 – 5в1/2)
Указание: а – в = (а1/2)2– (в1/2)2
Вариант 3
1. Сократите дробь
а) (х1/2 – х1/4)/х3/4
Указание: х1/4 вынести за скобку
б) (а1/2 – в1/2)/(4а1/4 – 4в1/4)
Вариант 4
Сократите дробь
а) 10/ (10 – 101/2)
б) (а - в)/(а2/3 + а1\3в1/3+ В 1/3)
Разделы: Математика
Класс: 9
ЦЕЛЬ: Закрепить и усовершенствовать навыки применения свойств степени с рациональным показателем; развивать навыки выполнения простейших преобразований выражений, содержащих степени с дробным показателем.
ТИП УРОКА: урок закрепления и применения знаний по данной теме.
УЧЕБНИК: Алгебра 9 под ред. С.А. Теляковского.
ХОД УРОКА
Вступительное слово учителя
“Люди, незнакомые с алгеброй, не могут представить себе тех удивительных вещей, которых можно достигнуть... при помощи названной науки”. Г.В. Лейбниц
Алгебра открывает перед нами двери в лабораторный комплекс “Степень с рациональным показателем”.
1. Фронтальный опрос
1) Дайте определение степени с дробным показателем.
2) Для какого дробного показателя определена степень с основанием равным нулю?
3) Определится ли степень с дробным показателем для отрицательного основания?
Задание: Представьте число 64 в виде степени с основанием - 2; 2; 8.
Куб какого числа равен 64?
Существует ли еще какой-нибудь способ представления числа 64 в виде степени с рациональным показателем?
2. Работа по группам
1 группа. Докажите, что выражения (-2) 3/4 ; 0 -2 не имеют смысла.
2 группа. Представьте степень с дробным показателем в виде корня: 2 2/3 ; 3 -1|3 ; -в 1,5 ; 5а 1/2 ; (x-y) 2/3 .
3 группа. Представьте в виде степени с дробным показателем: v3; 8 vа 4 ; 3v2 -2 ; v(x+y) 2/3 ; вvв.
3. Перейдем в лабораторию “Действие над степенями”
Частые гости лаборатории - астрономы. Они приносят свои “астрономические числа”, подвергают их алгебраической обработке и получают полезные результаты
Например, расстояние от Земли до туманности Андромеды выражается числом
95000000000000000000 = 95 10 18 км;
оно называется квинтиллион.
Масса солнца в граммах выражается числом 1983 10 30 гр - нональон.
Кроме этого, в лабораторию попадают и другие серьезные задачи. Например, часто возникает проблема вычисления выражений вида:
а) ; б) ; в) .
Сотрудники лаборатории производят такие вычисления наиболее удобным способом.
Вы можете подключиться к работе. Для этого повторим свойства степеней с рациональными показателями:
А теперь вычислите или упростите выражение, применяя свойства степеней с рациональными показателями:
1 группа:
2 группа:
3 группа:
Проверка: по одному человеку от группы у доски.
4. Задание на сравнение
Как, применяя свойства степеней, сравнить выражения 2 100 и 10 30 ?
Ответ:
2 100 =(2 10) 10 =1024 10 .
10 30 =(10 3) 10 =1000 10
1024 10 >1000 10
2 100 >10 30
5. А сейчас я приглашаю вас в лабораторию “Исследование степеней”.
Какие преобразования мы можем выполнять над степенями?
1) Представьте число 3 в виде степени с показателем 2; 3; -1.
2) Каким способом можно разложить на множители выражения а-в; в+в 1/2 ; а-2а 1/2 ; 2-х 2 ?
3) Сократите дробь с последующей взаимопроверкой:
4) Объясните выполненные преобразования и найдите значение выражения:

6. Работа с учебником. № 611(г, д, е).
1 группа: (г).
2 группа: (д).
3 группа: (е).
№ 629 (а, б).
Взаимопроверка.
7. Выполняем практикум (самостоятельная работа).
Даны выражения:

При сокращении каких дробей применяются формулы сокращенного умножения и вынесение за скобки общего множителя?
1 группа: № 1, 2, 3.
2 группа: № 4, 5, 6.
3 группа: № 7, 8, 9.
При выполнении задания можно пользоваться рекомендациями.
- Если в записи примера есть как степени с рациональным показателем, так и корни n-й степени, то запишите корни n-й степени в виде степеней с рациональным показателем.
- Постарайтесь упростить выражение, над которым выполняются действия: раскрытие скобок, применение формулы сокращенного умножения, переход от степени с отрицательным показателем к выражению, содержащему степени с положительным показателем.
- Определите порядок выполнения действий.
- Выполните действия, соблюдая порядок их выполнения.
Оценивает учитель, собрав тетради.
8. Домашнее задание: № 624, 623.
 Ударение в английском языке
Ударение в английском языке 10 слов с ударением на 1 слог
10 слов с ударением на 1 слог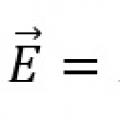 Закон Ома для замкнутой цепи и неоднородного участка цепи
Закон Ома для замкнутой цепи и неоднородного участка цепи