Круг деленный на 9 частей. Деление окружности на равные части и построение правильных вписанных многоугольников
Деление окружности на три равные части. Устанавливают угольник с углами 30 и 60° большим катетом параллельно одной из центровых линий. Вдоль гипотенузы из точки 1 (первое деление) проводят хорду (рис. 2.11, а ), получая второе деление – точку 2. Перевернув угольник и проведя вторую хорду, получают третье деление – точку 3 (рис. 2.11, б ). Соединив точки 2 и 3; 3 и 1 прямыми, получают равносторонний треугольник.
Рис. 2.11.
а, б – с помощью угольника; в – с помощью циркуля
Ту же задачу можно решить с помощью циркуля. Поставив опорную ножку циркуля в нижний или верхний конец диаметра (рис. 2.11, в ), описывают дугу, радиус которой равен радиусу окружности. Получают первое и второе деления. Третье деление находится на противоположном конце диаметра.
Деление окружности на шесть равных частей
Раствор циркуля устанавливают равным радиусу R окружности. Из концов одного из диаметров окружности (из точек 1, 4 ) описывают дуги (рис. 2.12, а, б ). Точки 1, 2, 3, 4, 5, 6 делят окружность на шесть равных частей. Соединив их прямыми, получают правильный шестиугольник (рис. 2.12, б ).

Рис. 2.12.
Ту же задачу можно выполнить с помощью линейки и угольника с углами 30 и 60° (рис. 2.13). Гипотенуза угольника при этом должна проходить через центр окружности.

Рис. 2.13.
Деление окружности на восемь равных частей
Точки 1, 3, 5, 7 лежат на пересечении центровых линий с окружностью (рис. 2.14). Еще четыре точки находят с помощью угольника с углами 45°. При получении точек 2, 4, 6, 8 гипотенуза угольника проходит через центр окружности.

Рис. 2.14.
Деление окружности на любое число равных частей
Для деления окружности на любое число равных частей пользуются коэффициентами, приведенными в табл. 2.1.
Длину l хорды, которую откладывают на заданной окружности, определяют по формуле l = dk, где l – длина хорды; d – диаметр заданной окружности; k – коэффициент, определяемый по табл. 1.2.
Таблица 2.1
Коэффициенты для деления окружностей
Чтобы разделить окружность заданного диаметра 90 мм, например, на 14 частей, поступают следующим образом.
В первой графе табл. 2.1 находят число делений п, т.е. 14. Из второй графы выписывают коэффициент k, соответствующий числу делений п. В данном случае он равен 0,22252. Диаметр заданной окружности умножают на коэффициент и получают длину хорды l= dk = 90 0,22252 = 0,22 мм. Полученную длину хорды откладывают циркулем-измерителем 14 раз на заданной окружности.
Нахождение центра дуги и определение величины радиуса
Задана дуга окружности, центр и радиус которой неизвестны.
Для их определения нужно провести две непараллельные хорды (рис. 2.15, а ) и восставить перпендикуляры к серединам хорд (рис. 2.15, б ). Центр О дуги находится на пересечении этих перпендикуляров.

Рис. 2.15.
Сопряжения
При выполнении машиностроительных чертежей, а также при разметке заготовок деталей на производстве часто приходится плавно соединять прямые линии с дугами окружностей или дугу окружности с дугами других окружностей, т.е. выполнять сопряжение.
Сопряжением называют плавный переход прямой в дугу окружности или одной дуги в другую.
Для построения сопряжений надо знать величину радиуса сопряжений, найти центры, из которых проводят дуги, т.е. центры сопряжений (рис. 2.16). Затем нужно найти точки, в которых одна линия переходит в другую, т.е. точки сопряжений. При построении чертежа сопрягающиеся линии нужно доводить точно до этих точек. Точка сопряжения дуги окружности и прямой лежит на перпендикуляре, опущенном из центра дуги на сопрягаемую прямую (рис. 2.17, а ), или на линии, соединяющей центры сопрягаемых дуг (рис. 2.17, б ). Следовательно, для построения любого сопряжения дугой заданного радиуса нужно найти центр сопряжения и точку (точки ) сопряжения.

Рис. 2.16.

Рис. 2.17.
Сопряжение двух пересекающихся прямых дугой заданного радиуса. Даны пересекающиеся под прямым, острым и тупым углами прямые линии (рис. 2.18, а ). Нужно построить сопряжения этих прямых дугой заданного радиуса R.

Рис. 2.18.
Для всех трех случаев можно применять следующее построение.
1. Находят точку О – центр сопряжения, который должен лежать на расстоянии R от сторон угла, т.е. в точке пересечения прямых, проходящих параллельно сторонам угла на расстоянии R от них (рис. 2.18, б ).
Для проведения прямых, параллельных сторонам угла, из произвольных точек, взятых на прямых, раствором циркуля, равным R, делают засечки и к ним проводят касательные (рис. 2.18, б ).
- 2. Находят точки сопряжений (рис. 2.18, в). Для этого из точки О опускают перпендикуляры на заданные прямые.
- 3. Из точки О, как из центра, описывают дугу заданного радиуса R между точками сопряжений (рис. 2.18, в).
Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
В данной статье Вы узнаете как разделить окружность на 3-6, 4-8, 5-10 и n частей.
Как разделить окружность на 3 и 6 частей
Для деления окружности на 3, 6 и кратное им количество частей проводим окружность заданного радиуса и со ответствующие оси. Деление можно начинать от точки пересечения вертикальной или горизонтальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6 раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шестиугольник. Соединение точек через однудает равносторонний треугольник, и деление окружности на 3 равные части.
Деление окружности на 3-6 равных частей
Как разделить окружность на 5 и 10 частей
Для того чтобы разделить окружность на 5 и 10 равных частей необходимо построить правильный пятиугольник. Для его построения необходимо выполнить следующее. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки «а» в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке «b». Радиусом R3 из точки «1» проводят дугу окружности до пересечения с заданной окружностью (т. 5) и получают сторону правильного пятиугольника, затем откладывают полученное расстояние по окружности 5 раз до получения правильного пятиугольника. Расстояние «b-0» дает сторону правильного пятиугольник.

Деление окружности на 5-10 равных частей
___________________________________________________________________________________________________
Как разделить окружность на n — равных частей
Иначе необходимо построить правильный многоугольник с n количеством сторон. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки «1″ окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей, на которые мы делим данную окружность, например 9 . Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Провод им линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через четные (или нечетные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т. к. точки 1, 2,… 9 делят окружность на 9 (N) равных частей.

Деление окружности на n равные части
___________________________________________________________________________________________________
Деление окружности на произвольное число равных частей можно производить с помощью таблицы хорд, численное выражение которых определяется умножением радиуса данной окружности на коэффициент, соответствующий числу деления, представленный в таблице.
Таблица хорд (коэффициентов для деления окружности)
| Коэффициент | Число частей делений окружности | Коэффициент | Число частей делений окружности | Коэффициент | |
| 1 | 0,000 | 11 | 0,282 | 21 | 0,149 |
| 2 | 1,000 | 12 | 0,258 | 22 | 0,142 |
| 3 | 0,866 | 13 | 0,239 | 23 | 0,136 |
| 4 | 0,707 | 14 | 0,223 | 24 | 0,130 |
| 5 | 0,588 | 15 | 0,208 | 25 | 0,125 |
| 6 | 0,500 | 16 | 0,195 | 26 | 0,120 |
| 7 | 0,434 | 17 | 0,184 | 27 | 0,116 |
| 8 | 0,383 | 18 | 0,178 | 28 | 0,112 |
| 9 | 0,342 | 19 | 0,165 | 29 | 0,108 |
| 10 | 0,309 | 20 | 0,156 | 30 | 0,104 |
___________________________________________________________________________________________________
Как найти центр дуги окружности
Необходимо выполнить следующее: на данной дуге отмечаем четыре произвольные точки A, B, C, D и соединяем их попарно хордами AB и CD.

Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров дает центр данной дуги и соответствующей ей окружности.
Приближенное деление дуги окружности на произвольное число равныx частей можно выполнить при помощи циркуля методом последовательного приближения.

При выполнении графических работ приходится решать многие задачи на построение. Наиболее встречающиеся при этом задачи — деление отрезков прямой, углов и окружностей на равные части, построение различных сопряжений.
Деление окружности на равные части с помощью циркуля
Пользуясь радиусом, нетрудно разделить окружность и на 3, 5, 6, 7, 8, 12 равных участков.
Деление окружности на четыре равные части.
Штрихпунктирные центровые линии, проведенные перпендикулярно одна другой, делят окружность на четыре равные части. Последовательно соединив их концы, получим правильный четырехугольник (рис. 1).
Рис.1 Деление окружности на 4 равные части.
Деление окружности на восемь равных частей.
Чтобы разделить окружность на восемь равных частей, дуги, равные четвертой части окружности, делят пополам. Для этого из двух точек, ограничивающих четверть дуги, как из центров радиусов окружности выполняют засечки за ее пределами. Полученные точки соединяют с центром окружностей и на пересечении их с линией окружности получают точки, делящие четвертные участки пополам, т. е. получают восемь равных участков окружности (рис. 2).

Рис.2. Деление окружности на 8 равных частей.
Деление окружности на шестнадцать равных частей.
Разделив циркулем дугу, равную 1/8, на две равные части, нанесём засечки на окружность. Соединив все засечки, отрезками прямых, получим правильный шестнадцатиугольник.

Рис.3. Деление окружности на 16 равных частей.
Деление окружности на три равные части.
Чтобы разделить окружность радиуса R на 3 равные части, из точки пересечения центровой линии с окружностью (например, из точки А) описывают как из центра дополнительную дугу радиусом R. Получают точки 2 и 3. Точки 1, 2, 3 делят окружность на три равные части.

Рис. 4. Деление окружности на 3 равные части.
Деление окружности на шесть равных частей. Сторона правильного шестиугольника, вписанного в окружность, равна радиусу окружности (рис. 5.).
Для деления окружности на шесть равных частей надо из точек 1 и 4 пересечения центровой линии с окружностью сделать на окружности по две засечки радиусом R , равным радиусу окружности. Соединив полученные точки отрезками прямых, получим правильный шестиугольник.

Рис. 5. Деление окружности на 6 равных частей
Деление окружности на двенадцать равных частей.
Чтобы разделить окружность на двенадцать равных частей, надо окружность поделить на четыре части взаимно перпендикулярными диаметрами. Приняв точки пересечения диаметров с окружностью А , В , С , D за центры, величиной радиуса проводят четыре дуги до пересечения с окружностью. Полученные точки 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 и точки А , В , С , D разделяют окружность на двенадцать равных частей (рис. 6).

Рис. 6. Деление окружности на 12 равных частей
Деление окружности на пять равных частей
Из точки А проведем дугу тем же радиусом, что и радиус окружности до пересечения с окружностью - получим точку В . Опустив перпендикуляр с этой точки - получим точку С .Из точки С - середины радиуса окружности, как из центра, дугой радиуса СD сделаем засечку на диаметре, получим точку Е . Отрезок DЕ равен длине стороны вписанного правильного пятиугольника. Сделав радиусом DЕ засечки на окружности, получим точки деления окружности на пять равных частей.

Рис. 7. Деление окружности на 5 равных частей
Деление окружности на десять равных частей
Разделив окружность на пять равных частей, легко можно разделить окружность и на 10 равных частей. Проведя прямые от получившихся точек через центр окружности до противоположных сторон окружности - получим ещё 5 точек.

Рис. 8. Деление окружности на 10 равных частей
Деление окружности на семь равных частей
Чтобы разделить окружность радиуса R на 7 равных частей, из точки пересечения центровой линии с окружностью (например, из точки А ) описывают как из центра дополнительную дугу этим же радиусом R - получают точку В . Опустив перпендикуляр с точки В - получим точку С .Отрезок ВС равен длине стороны вписанного правильного семиугольника.

Рис. 9. Деление окружности на 7 равных частей
Для деления окружности пополам достаточно провести любой еедиаметр. Два взаимно перпендикулярных диаметра разделят окружность на четыре равные части (рисунок 28, а).Разделив каждую четвертую часть пополам, получают восьмые части, а при дальнейшем делении – шестнадцатые, тридцать вторые части и т. д. (рисунок 28, б).Если соединить прямымиточки деления, то можно получить стороны правильного вписанного квадрата(а 4 ), восьмиугольника (а 8 ) и т. д. (рисунок 28, в).
Рисунок 28
Деление окружности на 3, 6, 12 и т, д. равных частей, а также построение соответствующих правильных вписанных многоугольников осуществляют следующим образом. В окружности проводят два взаимно перпендикулярных диаметра 1–2 и 3–4 (рисунок 29 а). Из точек 1 и 2 как из центров описывают дуги радиусом окружности R до пересечения с ней в точках А, В, С и D . Точки A , B , 1, С, D и 2 делят окружность на шесть равных частей. Эти же точки, взятые через одну, разделят окружность на три равные части (рисунок 29, б). Для деления окружности на 12 равных частей описывают еще две дуги радиусом окружности из точек 3 и 4 (рисунок 29, в).

Рисунок 29
Построить правильные вписанные треугольник, шестиугольник и т. д. можно также с помощью линейки и угольника в 30 и 60°. На рисунке 30 приведено подобное построение для вписанного треугольника.

Рисунок 30
Деление окружности на семь равных частей и построение правильного вписанного семиугольника (рисунок 31) выполняют с помощью половины стороны вписанного треугольника, приблизительно равной стороне вписанного семиугольника.

Рисунок 31
Для деления окружности на пять или десятьравных частей проводят два взаимно перпендикулярных диаметра (рисунок 32, а). Радиус OA делят пополам и, получив точку В , описывают из нее дугу радиусом R=BC до пересечения ее в точке D с горизонтальным диаметром. Расстояние между точками C и D равно длине стороны правильного вписанного пятиугольника (а 5 ), а отрезок OD равен длине стороны правильного вписанного десятиугольника (а 10 ). Деление окружности на пять и десять равных частей, а также построение вписанных правильных пятиугольника и десятиугольника показаны на рисунке 32, б. Примером использования деления окружности на пять частей является пятиконечная звезда (рисунок 32, в).

Рисунок 32
На рисунке 33 приведен общий способ приближенного деления окружности на равные части . Пусть требуется разделить окружность на девять равных частей. В окружности проводят два взаимно перпендикулярных диаметра и вертикальный диаметр AB делят на девять равных частей с помощью вспомогательной прямой (рисунок 33, а). Из точки B описывают дугу радиусом R = AB, и на пересечении ее с продолжением горизонтального диаметра получают точки С и D . Из точек C и D через четные или нечетные точки деления диаметра AB проводят лучи. Точки пересечения лучей с окружностью разделят ее на девять равных частей (рисунок 33, б).
Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.
Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R.
Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D.
Части окружностей называются дугами .
Прямая СD, соединяющая две точки на окружности, называется хордой .
Прямая МN,которая имеет только одну общую точку с окружностью называется касательной .
Часть круга, ограниченная хордой СD и дугой, называется сигментом .
Часть круга, ограниченная двумя радиусами и дугой, называется сектором .
Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности .
Угол, образованный двумя радиусами КОА, называется центральным углом .
Два взаимно перпендикулярных радиуса составляют угол в 90 0 и ограничивают 1/4 окружности.
Деление окружности на части

Проводим окружность с горизонтальной и вертикальной осями, которые делят её на 4-ре равные части. Проведённые с помощью циркуля или угольника под 45 0 , две взаимно перпендикулярные линии делят окружность на 8-мь равных частей.
Деление окружности на 3 и 6 равных частей (кратные 3 трём)

Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну даёт равносторонний треугольник, и деление окружности на три равные части.

Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки "а" в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке "b". Радиусом R3 из точки "1" проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние "b-О" даёт сторону правильного десятиугольника.
Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)

Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки "1" окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через чётные (или нечётные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть (N) равных частей.

Для нахождения центра дуги окружности нужно выполнить следующие построения: на данной дуге отмечаем четыре произвольные точки А, В, С, D и соединяем их попарно хордами АВ и СD. Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров даёт центр данной дуги и соответствующей ей окружности.
 Ударение в английском языке
Ударение в английском языке 10 слов с ударением на 1 слог
10 слов с ударением на 1 слог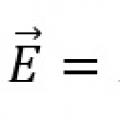 Закон Ома для замкнутой цепи и неоднородного участка цепи
Закон Ома для замкнутой цепи и неоднородного участка цепи