Трапеции высоту неверное формулу. Формулы нахождения диагоналей трапеции через высоту. Свойства отрезка, параллельного основаниям трапеции

Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.

Какую теорию необходимо помнить? Это:

Задачи с трапециями, которые имеются на блоге можно посмотреть здесь .

27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.

Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:

Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.

27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 0 , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.

Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?

Посмотрите: равнобедренная трапеция с углом при основании равным 60 0 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:

В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее

То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.

*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 180 0 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.

27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:

Отрезок EF является высотой трапеции, его нам нужно найти.

В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:

В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:

Таким образом EF=FO+OE=4+3=7.

Теперь важный нюанс!

В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.

А если бы в условии не было дано эскиза?

Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями:

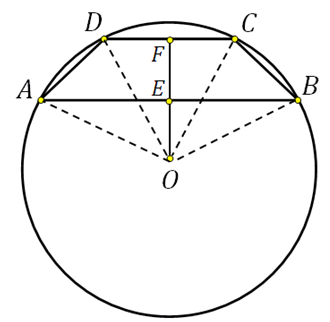
*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.

И решение будет «второго варианта» будет следующим.

По теореме Пифагора вычисляем OF:

Также вычислим OE:

Таким образом EF=FO–OE=4–3=1.

Конечно, в задаче с кратким ответом на ЕГЭ двух ответов быть не может, и подобная задача без эскиза дана не будет. Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием). Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.

27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.

Здесь сразу следует вспомнить свойство четырёхугольника описанного около окружности:

Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.

В материалах различных контрольных работ и экзаменов очень часто встречаются задачи на трапецию , решение которых требует знания ее свойств.

Выясним, какими же интересными и полезными для решения задач свойствами обладает трапеция.

После изучения свойства средней линии трапеции можно сформулировать и доказать свойство отрезка, соединяющего середины диагоналей трапеции . Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.

MO – средняя линия треугольника ABC и равна 1/2ВС (рис. 1).

MQ – средняя линия треугольника ABD и равна 1/2АD.

Тогда OQ = MQ – MO, следовательно, OQ = 1/2AD – 1/2BC = 1/2(AD – BC).

При решении многих задач на трапецию одним из основных приемов является проведение в ней двух высот.

Рассмотрим следующую задачу .

Пусть BT – высота равнобедренной трапеции ABCD с основаниями BC и AD, причем BC = a, AD = b. Найти длины отрезков AT и TD.

Решение.

Решение задачи не вызывает затруднения (рис. 2) , но оно позволяет получить свойство высоты равнобедренной трапеции, проведенной из вершины тупого угла : высота равнобедренной трапеции, проведенная из вершины тупого угла, делит большее основание на два отрезка, меньший из которых равен полуразности оснований, а больший – полусумме оснований.

При изучении свойств трапеции нужно обратить внимание на такое свойство, как подобие. Так, например, диагонали трапеции разбивают ее на четыре треугольника, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики. Это утверждение можно назвать свойством треугольников, на которые разбивается трапеция ее диагоналями . Причем первая часть утверждения доказывается очень легко через признак подобия треугольников по двум углам. Докажем вторую часть утверждения.

Треугольники BOC и COD имеют общую высоту (рис. 3) , если принять за их основания отрезки BO и OD. Тогда S BOC /S COD = BO/OD = k. Следовательно, S COD = 1/k · S BOC .

Аналогично, треугольники BOC и АОВ имеют общую высоту, если принять за их основания отрезки CO и OA. Тогда S BOC /S AOB = CO/OA = k и S А O В = 1/k · S BOC .

Из этих двух предложений следует, что S COD = S А O В.

Не будем останавливаться на сформулированном утверждении, а найдем связь между площадями треугольников, на которые разбивается трапеция ее диагоналями . Для этого решим следующую задачу.

Пусть точка O – точка пересечения диагоналей трапеции АBCD с основаниями BC и AD. Известно, что площади треугольников BOC и AOD равны соответственно S 1 и S 2 . Найти площадь трапеции.

Так как S COD = S А O В, то S АВС D = S 1 + S 2 + 2S COD .

Из подобия треугольников BОC и AOD следует, что ВО/OD = √(S₁/S 2).

Следовательно, S₁/S COD = BO/OD = √(S₁/S 2), а значит S COD = √(S 1 · S 2).

Тогда S АВС D = S 1 + S 2 + 2√(S 1 · S 2) = (√S 1 + √S 2) 2 .

С использованием подобия доказывается и свойство отрезка, проходящего через точку пересечения диагоналей трапеции параллельно основаниям .

Рассмотрим задачу :

Пусть точка O – точка пересечения диагоналей трапеции ABCD с основаниями BC и AD. BC = a, AD = b. Найти длину отрезка PK, проходящего через точку пересечения диагоналей трапеции параллельно основаниям. На какие отрезки делится PK точкой О (рис. 4)?

Из подобия треугольников AOD и BOC следует, что АO/OС = AD/BC = b/a.

Из подобия треугольников AOР и ACB следует, что АO/AС = PO/BC = b/(a + b).

Отсюда PO = BC · b / (a + b) = ab/(a + b).

Аналогично, из подобия треугольников DOK и DBC, следует, что OK = ab/(a + b).

Отсюда PO = OK и PK = 2ab/(a + b).

Итак, доказанное свойство можно сформулировать так: отрезок, параллельный основаниям трапеции, проходящий через точку пересечения диагоналей и соединяющий две точки на боковых сторонах, делится точкой пересечения диагоналей пополам. Его длина есть среднее гармоническое оснований трапеции.

Следующее свойство четырех точек : в трапеции точка пересечения диагоналей, точка пересечения продолжения боковых сторон, середины оснований трапеции лежат на одной линии.

Треугольники BSC и ASD подобны (рис. 5) и в каждом из них медианы ST и SG делят угол при вершине S на одинаковые части. Следовательно, точки S, T и G лежат на одной прямой.

Точно так же на одной прямой расположены точки T, O и G. Это следует из подобия треугольников BOC и AOD.

Значит, все четыре точки S, T, O и G лежат на одной прямой.

Так же можно найти длину отрезка разбивающего трапецию на две подобных.

Если трапеции ALFD и LBCF подобны (рис. 6), то a/LF = LF/b.

Отсюда LF = √(ab).

Таким образом, отрезок разбивающий трапецию на две подобные трапеции, имеет длину равную среднему геометрическому длин оснований .

Докажем свойство отрезка, делящего трапецию на две равновеликие .

Пусть площадь трапеции равна S (рис. 7). h 1 и h 2 – части высоты, а х – длина искомого отрезка.

Тогда S/2 = h 1 · (a + x)/2 = h 2 · (b + x)/2 и

S = (h 1 + h 2) · (a + b)/2.

Составим систему

{h 1 · (a + x) = h 2 · (b + x)
{h 1 · (a + x) = (h 1 + h 2) · (a + b)/2.

Решая данную систему, получим х = √(1/2(а 2 + b 2)).

Таким образом, длина отрезка, делящего трапецию на две равновеликие, равна√((а 2 + b 2)/2) (среднему квадратичному длин оснований).

Итак, для трапеции ABCD с основаниями AD и BC (BC = a, AD = b) доказали, что отрезок:

1) MN, соединяющий середины боковых сторон трапеции, параллелен основаниям и равен их полусумме (среднему арифметическому чисел a и b);

2) PK, проходящий через точку пересечения диагоналей трапеции параллельно основаниям, равен
2ab/(a + b) (среднему гармоническому чисел a и b);

3) LF, разбивающий трапецию на две подобные трапеции, имеет длину равную среднему геометрическому чисел a и b, √(ab);

4) EH, делящий трапецию на две равновеликие, имеет длину √((а 2 + b 2)/2) (среднее квадратичное чисел a и b).

Признак и свойство вписанной и описанной трапеции.

Свойство вписанной трапеции: трапеция может быть вписана в окружность в том и только в том случае, когда она равнобедренная.

Свойства описанной трапеции. Около окружности можно описать трапецию тогда и только тогда, когда сумма длин оснований равна сумме длин боковых сторон.

Полезные следствия того, что в трапецию вписана окружность:

1. Высота описанной трапеции равна двум радиусам вписанной окружности.

2. Боковая сторона описанной трапеции видна из центра вписанной окружности под прямым углом.

Первое очевидно. Для доказательства второго следствия необходимо установить, что угол COD прямой, что так же не составляет большого труда. Зато знание этого следствия позволяет при решении задач использовать прямоугольный треугольник.

Конкретизируем следствия для равнобедренной описанной трапеции :

Высота равнобедренной описанной трапеции есть среднее геометрическое оснований трапеции
h = 2r = √(ab).

Рассмотренные свойства позволят более глубоко познать трапецию и обеспечат успешность в решении задач на применение ее свойств.

Остались вопросы? Не знаете, как решать задачи на трапецию?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!

blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Тема урока

Трапеция

Цели урока

Продолжать знакомить с новыми определениями в геометрии;
Закрепить знания об уже изученных геометрических фигурах;
Познакомить с формулировкой и доказательствами свойств трапеции;
Обучить применению свойств различных фигур при решении задач и выполнении заданий;
Продолжать развивать у школьников внимание, логическое мышление и математическую речь;
Воспитывать интерес к предмету.

Задачи урока

Вызвать интерес к знаниям по геометрии;
Продолжать упражнять школьников в решении задач;
Вызвать познавательный интерес к урокам математики.

План урока

1. Повторить материал, изученный ранее.
2. Знакомство с трапецией, ее свойствами и признаками.
3. Решение задач и выполнение заданий.

Повторение ранее изученного материала

На предыдущем уроке вы знакомились с такой фигурой, как четырехугольник. Давайте закрепим пройденный материал и ответим на поставленные вопросы:

1. Сколько углов и сторон имеет 4-х угольник?
2. Сформулируйте определение 4-х угольника?
3. Какое название носят противоположные стороны 4-х угольника?
4. Какие виды четырехугольников вам известны? Перечислите их и дайте определение каждого из них.
5. Изобразите пример выпуклого и невыпуклого четырехугольника.

Трапеция. Общие свойства и определение

Трапеция - это такая четырехугольная фигура, у которой только одна пара противолежащих сторон параллельна.

В геометрическом определении к трапеции относится такой 4-х угольник, который имеет две параллельные стороны, а две другие – нет.

Название такой необычной фигуры, как «трапеция» произошло от слова «трапезион», что в переводе с греческого языка, обозначает слово «столик», от которого произошли также слово «трапеза» и другие родственные слова.

В некоторых случаях в трапеции пара противоположных сторон параллельна, а другая его пара не является параллельной. В таком случае трапеция носит название криволинейной.

Элементы трапеции

Трапеция состоит из таких элементов, как основание, боковые линии, средняя линия и ее высота.

Основанием трапеции называют ее параллельные стороны;
Боковыми сторонами называют две другие стороны трапеции, которые не есть параллельными;
Средней линией трапеции называют отрезок, который соединяет середины его боковых сторон;
Высотой трапеции считается расстояние между ее основаниями.

Виды трапеций

Задание:

1. Сформулируйте определение равнобедренной трапеции.
2. Какая трапеция называется прямоугольной?
3. Что значит остроугольная трапеция?
4. Какая трапеция относится к тупоугольной?

Общие свойства трапеции

Во-первых, средняя линия трапеции находится параллельно основанию фигуры и равняется ее полусумме;

Во-вторых, отрезок, который соединяет середины диагоналей 4-х угольной фигуры, равняется полуразности ее оснований;

В-третьих, в трапеции параллельно лежащие прямые, которые пересекают стороны угла данной фигуры, отсекают пропорциональные отрезки от сторон угла.

В-четвертых, в любого из видов трапеции сумма углов, которые прилегают к ее боковой стороне, равны 180°.

Где еще присутствует трапеция

Слово «трапеция» присутствует не только в геометрии, она имеет более широкое применение в повседневной жизни.

Это необычное слово мы можем встретить, просматривая спортивные соревнования гимнастов, выполняющих акробатические упражнения на трапеции. В гимнастике трапецией называют спортивный снаряд, который состоит из перекладины, подвешенной на двух веревках.

Также это слово можно услышать, занимаясь в спортивном зале или в среде людей, которые занимаются бодибилдингом, так как трапеции - это не только геометрическая фигура или спортивный акробатический снаряд, но и мощные мышцы спины, которые расположены сзади за шеей.

На рисунке изображена воздушная трапеция, которую изобрел для цирковых акробатов артист Джулиус Леотард еще в девятнадцатом веке во Франции. Вначале создатель этого номера устанавливал свой снаряд на небольшой высоте, но в итоге он был перенесен под самый купол цирка.

Воздушные гимнасты в цирке выполняют трюки перелетов из трапеции на трапецию, исполняют перекрёстные полёты, проделывают в воздухе сальто-мортале.

В конном виде спорта, трапецией называют упражнение для растяжки или потягивание тела лошади, которое очень полезно и приятно для животного. Во время стойки лошади в положении трапеции работает растяжка ног животного или мышц его спины. Это красивое упражнение мы можем наблюдать во время поклона или так называемого «переднего кранча», когда лошадь глубоко прогибается.

Задание: Наведите свои примеры о том, где еще в повседневной жизни можно услышать слова «трапеция»?

А известно ли вам, что впервые в 1947 году известный французский модельер Кристиан Диор произвел показ мод, в котором присутствовал силуэт юбки-трапеции. И хотя уже прошло более шестидесяти лет, этот силуэт до сих пор в моде, и не теряет своей актуальности, и по сей день.

В гардеробе английской королевы юбка-трапеция стала непременным предметом и ее визитной карточкой.

Напоминающая геометрическую форму трапеции, юбка с одноименным названием прекрасно сочетается с любыми кофточками, блузами, топами и пиджаками. Классичность и демократичность этого популярного фасона позволяет ее носить и со строгими пиджаками и немного легкомысленными топами. В такой юбке будет уместно появляться как в офисе, так и на дискотеке.

Задачи с трапецией

Для облегчения решения задач с трапециями важно помнить несколько основных правил:

Во-первых, проведите две высоты: ВF и СК.

В одном из случаев, в результате вы получите прямоугольник – ВСFК из чего понятно, что FК=ВС.

АD=АF+FК+КD, отсюда АD=АF+ВС+КD.

К тому же сразу очевидно, что АВF и DСК – это прямоугольные треугольники.

Возможен еще такой вариант, когда трапеция не совсем стандартная, где

АD=АF+FD=АF+FК–DК=АF+ВС–DК.

Но самый простой вариант, если наша трапеция – равнобедренная. Тогда решать задачу становиться еще легче, потому что АВF и DСК – это прямоугольные треугольники, и они равны. АВ=СD, так как трапеция равнобедренная, а ВF=СК, как высоты трапеции. Из равенства треугольников следует равенство соответствующих сторон.

Трапецией называется выпуклый четырехугольник, у которого одна пара противоположных сторон параллельна друг другу, а другая - нет.

Исходя из определения трапеции и признаков параллелограмма, параллельные стороны трапеции не могут быть равны друг другу. Иначе другая пара сторон также стала бы параллельной и равной друг другу. В таком случае мы имели бы дело с параллелограммом.

Параллельные противоположные стороны трапеции называют ее основаниями . То есть у трапеции два основания. Непараллельные противоположные стороны трапеции называют ее боковыми сторонами .

В зависимости от того, какие боковые стороны, какие углы они образуют с основаниями, выделяют различные виды трапеций. Чаще всего трапеции делят на неравнобедренные (разнобокие), равнобедренные (равнобокие) и прямоугольные.

У разнобоких трапеций боковые стороны не равны друг другу. При этом с большим основанием они обе могут образовывать только острые углы, или один угол будет тупым, а второй острым. В первом случае трапецию называют остроугольной , во втором - тупоугольной .

У равнобедренных трапеций боковые стороны равны друг другу. При этом с большим основанием они могут образовывать только острые углы, т.е. все равнобедренные трапеции остроугольные. Поэтому их не делят на остроугольные и тупоугольные.

У прямоугольных трапеций одна боковая сторона перпендикулярна основаниям. Вторая сторона не может быть им перпендикулярна, т. к. в этом случае мы имели бы дело с прямоугольником. В прямоугольных трапециях неперпендикулярная боковая сторона образует с большим основанием всегда острый угол. Перпендикулярная боковая сторона перпендикулярна обеим основаниям, т. к. основания параллельны.

Для обозначения элементов трапеции существует своя терминология. Параллельные стороны этой геометрической фигуры называются ее основаниями. Как правило, они не равны между собой. Однако существует , в котором про непараллельные стороны ничего не говорится. Поэтому некоторые математики рассматривают в качестве частного случая трапеции параллелограмм. Однако в подавляющем большинстве учебников все-таки упоминается непараллельность второй пары сторон, которые называются боковыми.

Существует несколько видов трапеций. Если ее боковые стороны между собой равны, то трапеция называется равнобедренной или равнобокой. Одна из боковых сторон может быть перпендикулярна основаниям. Соответственно, в этом случае фигура будет прямоугольной.

Есть еще несколько линий, определяющих трапеции и помогающих вычислениям других параметров. Разделите боковые стороны пополам и проведите через полученные точки прямую. Вы получите среднюю линию трапеции. Она параллельна основаниям и их полусумме. Выразить ее можно формулой n=(a+b)/2, где n – длина , а и b - длины оснований. Средняя линия - очень важный параметр. Например, через нее можно выразить площадь трапеции, которая равна длине средней линии, умноженной на высоту, то есть S=nh.

Проведите из угла между боковой стороной и более коротким основанием перпендикуляр к длинному основанию. Вы получите высоту трапеции. Как и любой перпендикуляр, высота - кратчайшее расстояние между заданными прямыми.

У есть дополнительные свойства, которые необходимо знать. Углы между боковыми сторонами и основанием у такой между собой. Кроме того, равны ее диагонали, что легко , сравнив образованные ими треугольники.

Разделите основания пополам. Найдите точку пересечения диагоналей. Продолжите боковые стороны до их пересечения. У вас получатся 4 точки, через которые можно провести прямую, притом только одну.

Одним из важных свойств любого четырехугольника является возможность построить вписанную или описанную окружность. С трапецией это получается не всегда. Вписанная окружность получится только в том случае, если сумма оснований равна сумме боковых сторон. Описать окружность можно только вокруг равнобедренной трапеции.

Цирковая трапеция может быть стационарной и подвижной. Первая - это небольшая круглая перекладина. Она с двух сторон крепится железными прутьями к куполу цирка. Подвижная трапеция крепится тросами или канатами, она может свободно качаться. Встречаются двойные и даже тройные трапеции. Этим же термином называется и сам жанр цирковой акробатики.

Термин «трапеция»