Модуль десятичной дроби определение. Десятичные дроби: определения, запись, примеры, действия с десятичными дробями

Данный материал мы посвятим такой важной теме, как десятичные дроби. Сначала определимся с основными определениями, приведем примеры и остановимся на правилах десятичной записи, а также на том, что из себя представляют разряды десятичных дробей. Далее выделим основные виды: конечные и бесконечные, периодические и непериодические дроби. В финальной части мы покажем, как точки, соответствующие дробным числам, расположены на оси координат.

Yandex.RTB R-A-339285-1

Что такое десятичная запись дробных чисел

Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая.

Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля.

Какие можно привести примеры дробных чисел в десятичной записи? Это может быть 34 , 21 , 0 , 35035044 , 0 , 0001 , 11 231 552 , 9 и др.

В некоторых учебниках можно встретить использование точки вместо запятой (5 . 67 , 6789 . 1011 и др.) Это вариант считается равнозначным, но он более характерен для англоязычных источников.

Определение десятичных дробей

Основываясь на указанном выше понятии десятичной записи, мы можем сформулировать следующее определение десятичных дробей:

Определение 1

Десятичные дроби представляют собой дробные числа в десятичной записи.

Для чего нам нужна запись дробей в такой форме? Она дает нам некоторые преимущества перед обыкновенными, например, более компактную запись, особенно в тех случаях, когда в знаменателе стоят 1000 , 100 , 10 и др. или смешанное число. Например, вместо 6 10 мы можем указать 0 , 6 , вместо 25 10000 – 0 , 0023 , вместо 512 3 100 – 512 , 03 .

О том, как правильно представить в десятичном виде обыкновенные дроби с десятками, сотнями, тысячами в знаменателе, будет рассказано в рамках отдельного материала.

Как правильно читать десятичные дроби

Существуют некоторые правила чтения записей десятичных дробей. Так, те десятичные дроби, которым соответствуют их правильные обыкновенные эквиваленты, читаются почти так же, но с добавлением слов «ноль десятых» в начале. Так, запись 0 , 14 , которой соответствует 14 100 , читается как «ноль целых четырнадцать сотых».

Если же десятичной дроби можно поставить в соответствие смешанное число, то она читается тем же образом, как и это число. Так, если у нас есть дробь 56 , 002 , которой соответствует 56 2 1000 , мы читаем такую запись как «пятьдесят шесть целых две тысячных».

Значение цифры в записи десятичной дроби зависит от того, на каком месте она расположена (так же, как и в случае с натуральными числами). Так, в десятичной дроби 0 , 7 семерка – это десятые доли, в 0 , 0007 – десятитысячные, а в дроби 70 000 , 345 она означает семь десятков тысяч целых единиц. Таким образом, в десятичных дробях тоже существует понятие разряда числа.

Названия разрядов, расположенных до запятой, аналогичны тем, что существуют в натуральных числах. Названия тех, что расположены после, наглядно представлены в таблице:

Разберем пример.

Пример 1

У нас есть десятичная дробь 43 , 098 . У нее в разряде десятков находится четверка, в разряде единиц тройка, в разряде десятых – ноль, сотых – 9 , тысячных – 8 .

Принято различать разряды десятичных дробей по старшинству. Если мы движемся по цифрам слева направо, то мы будем идти от старших разрядов к младшим. Получается, что сотни старше десятков, а миллионные доли младше, чем сотые. Если взять ту конечную десятичную дробь, которую мы приводили в качестве примера выше, то в ней старшим, или высшим будет разряд сотен, а младшим, или низшим – разряд 10 -тысячных.

Любую десятичную дробь можно разложить по отдельным разрядам, то есть представить в виде суммы. Это действие выполняется так же, как и для натуральных чисел.

Пример 2

Попробуем разложить дробь 56 , 0455 по разрядам.

У нас получится:

56 , 0455 = 50 + 6 + 0 , 4 + 0 , 005 + 0 , 0005

Если мы вспомним свойства сложения, то сможем представить эту дробь и в других видах, например, как сумму 56 + 0 , 0455 , или 56 , 0055 + 0 , 4 и др.

Что такое конечные десятичные дроби

Все дроби, о которых мы говорили выше, являются конечными десятичными дробями. Это означает, что количество цифр, расположенное у них после запятой, является конечным. Выведем определение:

Определение 1

Конечные десятичные дроби представляют собой вид десятичных дробей, у которых после знака запятой стоит конечное число знаков.

Примерами таких дробей могут быть 0 , 367 , 3 , 7 , 55 , 102567958 , 231 032 , 49 и др.

Любую из этих дробей можно перевести либо в смешанное число (если значение их дробной части отличается от нуля), либо в обыкновенную дробь (при нулевой целой части). Тому, как это делается, мы посвятили отдельный материал. Здесь просто укажем пару примеров: так, конечную десятичную дробь 5 , 63 мы можем привести к виду 5 63 100 , а 0 , 2 соответствует 2 10 (или любая другая равная ей дробь, например, 4 20 или 1 5 .)

Но обратный процесс, т.е. запись обыкновенной дроби в десятичном виде, может быть выполнен не всегда. Так, 5 13 нельзя заменить на равную дробь с знаменателем 100 , 10 и др., значит, конечная десятичная дробь из нее не получится.

Основные виды бесконечных десятичных дробей: периодические и непериодические дроби

Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.

Определение 2

Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.

Очевидно, что полностью такие числа записаны быть просто не могут, поэтому мы указываем лишь часть из них и дальше ставим многоточие. Это знак говорит о бесконечном продолжении последовательности знаков после запятой. Примерами бесконечных десятичных дробей могут быть 0 , 143346732 … , 3 , 1415989032 … , 153 , 0245005 … , 2 , 66666666666 … , 69 , 748768152 … . и т.д.

В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.

Определение 3

Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.

К примеру, для дроби 3 , 444444 … . периодом будет цифра 4 , а для 76 , 134134134134 … – группа 134 .

Какое же минимальное количество знаков допустимо оставить в записи периодической дроби? Для периодических дробей достаточно будет записать весь период один раз в круглых скобках. Так, дробь 3 , 444444 … . правильно будет записать как 3 , (4) , а 76 , 134134134134 … – как 76 , (134) .

В целом записи с несколькими периодами в скобках будут иметь точно такой же смысл: к примеру, периодическая дробь 0 , 677777 – это то же самое, что 0 , 6 (7) и 0 , 6 (77) и т.д. Также допустимы записи вида 0 , 67777 (7) , 0 , 67 (7777) и др.

Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.

То есть для указанной выше дроби основной будем считать запись 0 , 6 (7) , а, например, в случае с дробью 8 , 9134343434 будем писать 8 , 91 (34) .

Если знаменатель обыкновенной дроби содержит простые множители, не равные 5 и 2 , то при переводе в десятичную запись из них получатся бесконечные дроби.

В принципе, любую конечную дробь мы можем записать в виде периодической. Для этого нам просто нужно добавить справа бесконечно много нулей. Как это выглядит в записи? Допустим, у нас есть конечная дробь 45 , 32 . В периодическом виде она будет выглядеть как 45 , 32 (0) . Это действие возможно потому, что добавление нулей справа в любую десятичную дробь дает нам в результате равную ей дробь.

Отдельно следует остановиться на периодических дробях с периодом 9 , например, 4 , 89 (9) , 31 , 6 (9) . Они являются альтернативной записью схожих дробей с периодом 0 , поэтому их часто заменяют при письме именно дробями с нулевым периодом. При этом к значению следующего разряда добавляют единицу, а в круглых скобках указывают (0) . Равенство получившихся чисел легко проверить, представив их в виде обыкновенных дробей.

К примеру, дробь 8 , 31 (9) можно заменить на соответствующую ей дробь 8 , 32 (0) . Или 4 , (9) = 5 , (0) = 5 .

Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.

Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.

Определение 4

К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.

Иногда непериодические дроби выглядят очень похожими на периодические. Например, 9 , 03003000300003 … на первый взгляд кажется имеющей период, однако подробный анализ знаков после запятой подтверждает, что это все же непериодическая дробь. С такими числами надо быть очень внимательным.

Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.

Основные действия с десятичными дробями

С десятичными дробями можно производить следующие действия: сравнение, вычитание, сложение, деление и умножение. Разберем каждое из них отдельно.

Сравнение десятичных дробей может быть сведено к сравнению обыкновенных дробей, которые соответствуют исходным десятичным. Но бесконечные непериодические дроби свести к такому виду нельзя, а перевод десятичных дробей в обыкновенные зачастую является трудоемкой задачей. Как же быстро произвести действие сравнения, если нам нужно сделать это по ходу решения задачи? Удобно сравнивать десятичные дроби по разрядам таким же образом, как мы сравниваем натуральные числа. Этому методу мы посвятим отдельную статью.

Чтобы складывать одни десятичные дроби с другими, удобно использовать метод сложения столбиком, как для натуральных чисел. Чтобы складывать периодические десятичные дроби, необходимо предварительно заменить их обыкновенными и считать по стандартной схеме. Если же по условиям задачи нам надо сложить бесконечные непериодические дроби, то нужно перед этим округлить их до некоторого разряда, а потом уже складывать. Чем меньше разряд, до которого мы округляем, тем выше будет точность вычисления. Для вычитания, умножения и деления бесконечных дробей предварительное округление также необходимо.

Нахождение разности десятичных дробей обратно действию сложения. По сути, с помощью вычитания мы можем найти такое число, сумма которого с вычитаемой дробью даст нам уменьшаемую. Подробнее об этом расскажем в рамках отдельного материала.

Умножение десятичных дробей производится так же, как и для натуральных чисел. Для этого тоже подходит метод вычисления столбиком. Это действие с периодическими дробями мы опять же сводим к умножению обыкновенных дробей по уже изученным правилам. Бесконечные дроби, как мы помним, надо округлить перед подсчетами.

Процесс деления десятичных дробей является обратным процессу умножения. При решении задач мы также пользуемся подсчетами в столбик.

Можно установить точное соответствие между конечной десятичной дробью и точкой на оси координат. Выясним, как отметить точку на оси, которая будет точно соответствовать необходимой десятичной дроби.

Мы уже изучали, как построить точки, соответствующие обыкновенным дробям, а ведь десятичные дроби можно привести к такому виду. Например, обыкновенная дробь 14 10 – это то же самое, что и 1 , 4 , поэтому соответствующая ей точка будет удалена от начала отсчета в положительном направлении ровно на такое же расстояние:

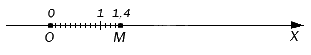
Можно обойтись без замены десятичной дроби на обыкновенную, а взять на основу метод разложения по разрядам. Так, если нам надо отметить точку, координата которой будет равна 15 , 4008 , то мы предварительно представим это число в виде суммы 15 + 0 , 4 + , 0008 . Для начала отложим от начала отсчета 15 целых единичных отрезков в положительном направлении, потом 4 десятых доли одного отрезка, а потом 8 десятитысячных долей одного отрезка. В итоге мы получим точку координат, которой соответствует дробь 15 , 4008 .

Для бесконечной десятичной дроби лучше пользоваться именно этим способом, поскольку он позволяет приблизиться к нужной точке сколь угодно близко. В некоторых случаях можно построить и точное соответствие бесконечной дроби на оси координат: так, 2 = 1 , 41421 . . . , и с этой дробью может быть соотнесена точка на координатном луче, удаленная от 0 на длину диагонали квадрата, сторона которого будет равна одному единичному отрезку.

Если мы находим не точку на оси, а десятичную дробь, соответствующую ей, то это действие называется десятичным измерением отрезка. Посмотрим, как правильно это сделать.

Допустим, нам нужно попасть от нуля в заданную точку на оси координат (или максимально приблизиться в случае с бесконечной дробью). Для этого мы постепенно откладываем единичные отрезки от начала координат, пока не попадем в нужную точку. После целых отрезков при необходимости отмеряем десятые, сотые и более мелкие доли, чтобы соответствие было максимально точным. В итоге мы получили десятичную дробь, которая соответствует заданной точке на оси координат.

Выше мы приводили рисунок с точкой M . Посмотрите на него еще раз: чтобы попасть в эту точку, нужно отмерить от нуля один единичный отрезок и четыре десятых доли от его, поскольку этой точке соответствует десятичная дробь 1 , 4 .

Если мы не можем попасть в точку в процессе десятичного измерения, то значит, что ей соответствует бесконечная десятичная дробь.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

В швейной мастерской было 5 цветов ленты. Красной ленты было больше, чем синей на 2,4 метра, но меньше, чем зеленой на 3,8 метра. Белой ленты было больше, чем черной на 1,5 метра, но меньше, чем зеленой на 1,9 метра. Сколько метров ленты всего было в мастерской, если белой было 7,3 метра?

Решение

1) 7,3 + 1,9 = 9,2 (м) зеленой ленты было в мастерской;
2) 7,3 – 1,5 = 5,8 (м) черной ленты;
3) 9,2 – 3,8 = 5,4 (м) красной ленты;
4) 5,4 - 2,4 = 3 (м) синей ленты;
5) 7,3 + 9,2 + 5,8 + 5,4 + 3 = 30,7 (м).
Ответ: всего в мастерской было 30,7 метров ленты.

Задача 2

Длина прямоугольного участка составляет 19,4 метра, а ширина на 2,8 метра меньше. Вычислите периметр участка.

Решение

1) 19,4 – 2,8 = 16,6(м) ширина участка;
2) 16,6 * 2 + 19,4 * 2 = 33,2 + 38,8 = 72(м).
Ответ: периметр участка равен 72 метра.

Задача 3

Длина прыжка кенгуру может достигать 13,5 метров в длину. Мировой рекорд для человека составляет 8,95 метров. Насколько дальше прыгает кенгуру?

Решение

1) 13,5 – 8,95 = 4,55 (м).
2) Ответ: кенгуру прыгает на 4,55 метра дальше.

Задача 4

Самая низкая температура на планете была зарегистрирована на станции Восток в Антарктиде, летом 21 июля 1983 года и составляла -89,2 ° C, а самая жаркая в городке Эль-Азизия, 13 сентября 1922 года составляла +57,8 ° C. Вычисли разницу между температурами.

Решение

1) 89,2 + 57,8 = 147° C.
Ответ: разница между температурами составляет 147° C.

Задача 5

Грузоподъемность фургона Газель составляет 1,5 тонн, а карьерного самосвала БелАЗ в 24 раза больше. Вычислите грузоподъемность самосвала БелАЗ.

Решение

1) 1,5 * 24 = 36 (тонн).
Ответ: грузоподъемность БелАЗа 36 тонн.

Задача 6

Максимальная скорость движения Земли по своей орбите 30,27 км/сек, а скорость Меркурия на 17,73 км больше. С какой скоростью Меркурий движется по своей орбите?

Решение

1) 30,27 + 17,73 = 48 (км/сек).
Ответ: скорость движение Меркурия по орбите 48 км/сек.

Задача 7

Глубина Марианской впадины составляет 11,023 км, а высота самой высокой горы в мире - Джомолунгмы 8,848 км над уровнем моря. Вычисли разницу между этими двумя точками.

Решение

1) 11,023 + 8,848 = 19,871(км).
Ответ: 19, 871 км.

Задача 8

Для Коли, как и для любого здорового человека, нормальная температура тела 36,6 ° C, а для его четвероногого друга Шарика на 2,2 ° C больше. Какая температура для Шарика считается нормальной?

Решение

1) 36,6 + 2,2 = 38,8° C.
Ответ: для Шарика нормальная температура тела 38,8° C.

Задача 9

Маляр за 1 день покрасил 18,6 м² забора, а его помощник, на 4,4 м² меньше. Сколько всего м2 забора покрасит маляр и его помощник за рабочую неделю, если она равна пяти дням?

Решение

1) 18,6 – 4,4 = 14,2 (м²) покрасит за 1 день помощник маляра;
2) 14,2 + 18,6 = 32,8 (м²) покрасят за 1 день вместе;
3) 32,8 *5 = 164 (м²).
Ответ: за рабочую неделю маляр и его помощник вместе покрасят 164 м² забора.

Задача 10

От двух пристаней навстречу друг другу одновременно отошли два катера. Скорость одного катера 42,2 км/ч второго на 6 км/ч больше. Какое расстояние будет между катерами через 2,5 часа, если расстояние между пристанями 140,5 км?

Решение

1) 42,2 + 6 = 48,2 (км/ч) скорость второго катера;
2) 42,2 * 2,5 = 105,5 (км) преодолеет первый катер за 2,5 часа;
3) 48,2 * 2,5 = 120,5 (км) преодолеет второй катер за 2,5 часа;
4) 140,5 – 105,5 = 35 (км) расстояние от первого катера до противоположной пристани;
5) 140,5 – 120, 5 = 20 (км) расстояние от второго катера до противоположной пристани;
6) 35 + 20 = 55 (км);
7) 140 – 55 = 85 (км).
Ответ: между катерами будет 85 км.

Задача 11

Каждый день велосипедист преодолевает 30,2 км. Мотоциклист, если бы затрачивал столько же времени, преодолевал бы расстояние в 2,5 раза большее, чем велосипедист. Какое расстояние может преодолеть мотоциклист за 4 дня?

Решение

1) 30,2 * 2,5 = 75,5 (км) за 1 день преодолеет мотоциклист;
2) 75,5 * 4 = 302 (км).
Ответ: мотоциклист может преодолеть за 4 дня 302 км.

Задача 12

В магазине за 1 день было продано 18, 3 кг печенья, а конфет на 2,4 кг меньше. Сколько конфет и печенья вместе было продано в магазине за этот день?

Решение

1) 18,3 – 2, 4 = 15,9 (кг) конфет было продано в магазине;
2) 15,9 + 18,3 = 34,2 (кг).
Ответ: конфет и печенья всего было продано 34,2 кг.

В виде:

± d m … d 1 d 0 , d -1 d -2 …

где ± — знак дроби: или +, или -,

, — десятичная запятая, которая служит разделителем меж целой и дробной частями числа,

d k — десятичные цифры.

При этом порядок следования цифр до запятой (слева от неё) имеет конец (как min 1-на цифра), а после запятой (справа) — может быть и конечной (как вариант, цифр после запятой может вообще не быть), и бесконечной.

Значением десятичной дроби ± d m … d 1 d 0 , d -1 d -2 … есть действительное число:

которое равно сумме конечного либо бесконечного количества слагаемых.

Представление действительных чисел при помощи десятичных дробей есть обобщение записи целых чисел в десятичной системе счисления. В представлении целого числа десятичной дробью нет цифр после запятой, и т.о., это представление выглядит так:

± d m … d 1 d 0 ,

И это совпадает с записью нашего числа в десятичной системе счисления.

Десятичная дробь - это итог деления 1-цы на 10, 100, 1000 и так далее частей. Эти дроби довольно удобны для вычислений, т.к. они основываются на такой же позиционной системе , на которой построены счёт и запись целых чисел. Благодаря этому запись и правила действий с десятичными дробями практически такие же, как и для целых чисел.

Записывая десятичные дроби не нужно отмечать знаменатель, он определяется местом, занимаемым соответствующей цифрой. Вначале пишем целую часть числа, далее справа ставим десятичную точку. Первая цифра после десятичной точки обозначает число десятых, вторая - число сотых, третья - число тысячных и так далее. Цифры, которые расположены после десятичной точки, являются десятичными знаками .

Например: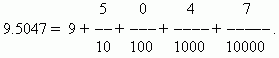

Одно из преимуществ десятичных дробей таково, что их очень просто можно привести к виду обыкновенных: число после десятичной точки (у нас это 5047) - это числитель ; знаменатель равен n -ой степени 10, где n - число десятичных знаков (у нас это n = 4 ):

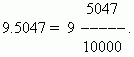
Когда в десятичной дроби нет целой части, значит, перед десятичной точкой ставим нуль:

Свойства десятичных дробей.

1. Десятичная дробь не изменяется, когда справа добавляются нули:

13.6 =13.6000.

2. Десятичная дробь не изменяется, когда удаляются нули, которые расположены в конце десятичной дроби:

0.00123000 = 0.00123.

Внимание! Нельзя удалять нули, которые расположенные НЕ в конце десятичной дроби!

3. Десятичная дробь увеличивается в 10, 100, 1000 и так далее раз, когда переносим десятичную точку на соответственно 1-ну, 2, 2 и так далее позиций правее:

3.675 → 367.5 (дробь увеличилась в сто раз).

4. Десятичная дробь становится меньше в десять, сто, тысячу и так далее раз, когда переносим десятичную точку на соответственно 1-ну, 2, 3 и так далее позиций левее:

1536.78 → 1.53678 (дробь стала меньше в тысячу раз).

Виды десятичных дробей.

Десятичные дроби делятся на конечные , бесконечные и периодические десятичные дроби .

Конечная десятичная дробь - это дробь, содержащая конечное количество цифр после запятой (или их там нет совсем), т.е. выглядит так:

Действительное число можно представить как конечную десятичную дробь лишь в том случае, если это число есть рациональным и при записи его несократимой дробью p/q знаменатель q не имеет простых делителей, которые отличны от 2 и 5.

Бесконечная десятичная дробь .

Содержит бесконечно повторяющуюся группу цифр, которая называется периодом . Период записывается в скобках. Например, 0.12345123451234512345… = 0.(12345) .

Периодическая десятичная дробь - это такая бесконечная десятичная дробь, в которой последовательность цифр после запятой, начиная с некоторого места, является периодически повторяющейся группой цифр. Иными словами, периодическая дробь — десятичная дробь, выглядящая так:

Подобную дробь обычно кратко записывают так:

Группа цифр b 1 … b l , которая повторяется, является периодом дроби , число цифр в этой группе является длиной периода .

Когда в периодической дроби период идет сразу после запятой, значит, дробь является чистой периодической . Когда между запятой и 1-ым периодом есть цифры, то дробь является смешанной периодической , а группа цифр после запятой до 1-го знака периода — предпериодом дроби .

Например , дробь 1,(23) = 1,2323… есть чистой периодической, а дробь 0,1(23)=0,12323… — смешанной периодической.

Основное свойство периодических дробей , благодаря которому их выделяют из всей совокупности десятичных дробей, заключается в том, что периодические дроби и лишь они представляют рациональные числа . Точнее, имеет место следующее:

Любая бесконечная периодическая десятичная дробь представляет рациональное число. Обратно, когда рациональное число раскладывается в бесконечную десятичную дробь, значит, эта дробь будет периодической.

ДЕСЯТИЧНЫЕ ДРОБИ. ДЕЙСТВИЯ НАД ДЕСЯТИЧНЫМИ ДРОБЯМИ

(урок-обобщение)

Тумышева Замира Тансыкбаевна, учитель математики, школа-гимназия №2

г. Хромтау Актюбинской области Республика Казахстан

Данная разработка урока предназначена как урок-обобщение по главе «Действия над десятичными дробями». Её можно использовать как в 5 классах, так и в 6 классах. Урок проводится в игровой форме.

Десятичные дроби. Действия над десятичными дробями. (урок-обобщение)

Цель :

Отработка умений и навыков сложения, вычитания, умножения и деления десятичных дробей на натуральные числа и на десятичную дробь

Создание условий для развития навыков самостоятельной работы, самоконтроля и самооценки, развития интеллектуальных качеств: внимания, воображения, памяти, умения анализировать и обобщать

Привить познавательный интерес к предмету и выработать уверенность в своих силах

ПЛАН УРОКА:

1. Организационная часть.

3. Тема и цель нашего урока.

4. Игра «К заветному флажку!»

5. Игра «Числовая мельница».

6. Лирическое отступление.

7. Проверочная работа.

8. Игра «Шифровка» (работа в парах)

9. Подведение итогов.

10. Домашнее задание.

1. Организационная часть. Здравствуйте. Присаживайтесь.

2. Обзор правил выполнения арифметических действий с десятичными дробями.

Правило сложения и вычитания десятичных дробей:

1) уравнять количество знаков после запятой в этих дробях;

2) записать друг под другом так, чтобы запятая была под запятой;

3) не замечая запятой, выполнить действие (сложение или вычитание), и поставить в результате запятую под запятыми.

3,455 + 0,45 = 3,905 3,5 + 4 = 7,5 15 – 7,88 = 7,12 4,57 - 3,2 = 1,37

3,455 + 3,5 _15,00 _ 4,57

0,450 4,0 7,88 3,20

3,905 7,5 7,12 1,37

При сложении и вычитании натуральные числа записывают как десятичную дробь с десятичными знаками, равными нулю

Правило умножения десятичных дробей:

1) не обращая внимания на запятую, умножить числа;

2) в полученном произведении отделить запятой столько цифр справа налево, сколько их отделено запятой в десятичных дробях.

При умножении десятичной дроби на разрядные единицы (10, 100, 1000 и т.п.) запятая переносится вправо на столько чисел, сколько нулей в разрядной единице

17,25 · 4 = 69

х 1 7,2 5

6 9,0 0

15,256 · 100 = 1525,6

,5 · 0,52 = 2,35

Х 0,5 2

4,5

2 7 0

2 0 8__

2,3 5 0

При умножении натуральные числа записывают как натуральные числа.

Правило деления десятичных дробей на натуральное число:

1) разделить целую часть делимого, поставить в частном запятую;

2) продолжить деление.

При делении к остатку сносим только по одному числу из делимого.

Если в процессе деления десятичной дроби останется остаток, то приписав к нему нужное число нулей, продолжим деление до тех пор, пока в остатке не получится нуль.

15,256: 100 = 0,15256

0,25: 1000 = 0,00025

Ри делении десятичной дроби на разрядные единицы (10, 100, 1000 и т.п.) запятая переносится влево на столько чисел, сколько нулей в разрядной единице.

18,4: 8 = 2,3

_ 18,4 І_8_

16 2,3

2 4

22,2: 25 = 0,88

22,2 І_25_

0 0,888

22 2

20 0

2 20

2 00

200

3,56: 4 = 0,89

3,56 І_4_

0 0,89

3 5

3 2

При делении натуральные числа записывают как натуральные числа.

Правило деления десятичных дробей на десятичную дробь:

1) перенесём запятую в делителе вправо так, чтобы получилось натуральное число;

2) запятую в делимом перенесём вправо настолько чисел, насколько перенесли в делителе;

3) производим деление десятичной дроби на натуральное число.

3,76: 0,4 = 9, 4

_ 3,7,6 І_0,4,_

3 6 9, 4

1 6

Игра «К заветному флажку!»

Правила игры: Из каждой команды к доске вызываются по одному ученику, которые производят устный счет с нижней ступеньки. Решивший один пример отмечает ответ в таблице. Дальше его сменяет другой член команды. Происходит движение вверх - к заветному флажку. Учащиеся на местах устно проверяют результаты своих игроков. При неправильном ответе к доске выходит другой член команды, чтобы продолжить решение заданий. Вызывают для работы у доски учеников капитаны команд. Выигрывает та команда, которая при наименьшем количестве учащихся первой достигнет флажка.

Игра «Числовая мельница»

Правила игры: В кружках мельницы записаны числа. На стрелках, соединяющих кружки, указаны действия. Задание состоит в том, чтобы выполнить последовательно действия, продвигаясь по стрелке от центра к внешней окружности. Выполняя последовательно действия по указанному маршруту, вы найдете ответ в одном из кружков внизу. Результат выполнения действий по каждой стрелке записывается в овале рядом.

Лирическое отступление.

Стихотворение Лифшица «Три десятых»

Это кто

Из портфеля

Швыряет в досаде

Ненавистный задачник,

Пенал и тетради

И суёт свой дневник.

Не краснея при этом,

Под дубовый буфет.

Чтоб лежал под буфетом?..

Познакомьтесь, пожалуйста:

Костя Жигалин.

Жертва вечных придирок, -

Он снова провален.

И шипит,

На растрёпанный

Глядя задачник:

Просто мне не везёт!

Просто я неудачник!

В чём причина

Обиды его и досады?

Что ответ не сошёлся

Лишь на три десятых.

Это сущий пустяк!

И к нему, безусловно,

Придирается

Строгая

Марья Петровна.

Три десятых...

Скажи про такую ошибку -

И, пожалуй, на лицах

Увидишь улыбку.

Три десятых...

И всё же об этой ошибке

Я прошу вас

Послушать меня

Без улыбки.

Если б, строя ваш дом.

Тот, в котором живёте.

Архитектор

Немножко

Ошибся

В расчёте, -

Что б случилось.

Ты, знаешь ли, Костя Жигалин?

Этот дом

Превратился бы

В груду развалин!

Ты вступаешь на мост.

Он надёжен и прочен.

А не будь инженер

В чертежах своих точен, -

Ты бы, Костя,

Свалившись

в холодную реку,

Не сказал бы спасибо

Тому человеку!

Вот турбина.

В ней вал

Токарями расточен.

Если б токарь

В работе

Не очень был точен, -

Совершилось бы, Костя,

Большое несчастье:

Разнесло бы турбину

На мелкие части!

Три десятых -

И стены

Возводятся

Косо!

Три десятых -

И рухнут

Вагоны

С откоса!

Ошибись

Только на три десятых

Аптека, -

Станет ядом лекарство,

Убьёт человека!

Мы громили и гнали

Фашистскую банду.

Твой отец подавал

Батарее команду.

Ошибись он прилетом

Хоть на три десятых, -

Не настигли б снаряды

Фашистов проклятых.

Ты подумай об этом,

Мой друг, хладнокровно

И скажи.

Не права ль была

Марья Петровна?

Если честно

Подумаешь, Костя, об этом.

То недолго лежать

Дневнику под буфетом!

Проверочная работа по теме «Десятичные дроби» (математика -5)

На экране последовательно появятся 9 слайдов. Учащиеся в тетрадях записывают номер варианта и ответы на вопрос. Например, Вариант 2

1. С; 2. А; и т.п.

ВОПРОС 1

Вариант 1

При умножении десятичной дроби на 100, нужно в этой дроби перенести запятую:

А. влево на 2 цифры; В. вправо на 2 цифры; С. не менять место запятой.

Вариант 2

При умножении десятичной дроби на 10, нужно в этой дроби перенести запятую:

А. вправо на 1 цифру; В. влево на 1 цифру; С. не менять место запятой.

ВОПРОС 2

Вариант 1

Сумма 6,27+6,27+6,27+6,27+6,27 в виде произведения записывается так:

А. 6,27 · 5; В. 6,27 · 6,27; С. 6,27 · 4.

Вариант 2

Сумма 9,43+9,43+9,43+9,43 в виде произведения записывается так:

А. 9,43 · 9,43; В. 6 · 9,43; С. 9,43 · 4.

ВОПРОС 3

Вариант 1

В произведении 72,43· 18 после запятой будет:

Вариант 2

В произведении 12,453· 35 после запятой будет:

А. 2 цифры; В. 0 цифр; С. 3 цифры.

ВОПРОС 4

Вариант 1

В частном 76,4: 2 после запятой будет:

А. 2 цифры; В. 0 цифр; С. 1 цифра.

Вариант 2

В частном 95,4: 6 после запятой будет:

А. 1 цифра; В. 3 цифры; С. 2 цифры.

ВОПРОС 5

Вариант 1

Найти значение выражения 34,5: х + 0,65· у, при х=10 у=100:

А. 35,15; В. 68,45; С. 9,95.

Вариант 2

Найти значение выражения 4,9 · х +525:у, при х=100 у=1000:

А. 4905,25; В. 529,9; С. 490,525.

ВОПРОС 6

Вариант 1

Площадь прямоугольника со сторонами 0,25 и 12 см равна

А. 3; В. 0,3; С. 30.

Вариант 2

Площадь прямоугольника со сторонами 0,5 и 36 см равна

А. 1,8; В. 18; С. 0,18.

ВОПРОС 7

Вариант 1

Из школы одновременно в противоположные стороны вышли два ученика. Скорость первого ученика 3,6 км\ч, скорость второго – 2,56 км\ч. Через 3 часа расстояние между ними будет равно :

А. 6,84 км; В. 18,48 км; С. 3,12 км

Вариант 2

Из школы одновременно в противоположные стороны выехали два велосипедиста. Скорость первого 11,6 км\ч, скорость второго – 13,06 км\ч. Через 4 часа расстояние между ними будет равно :

А. 5,84 км; В. 100,8 км; С. 98,64 км

Вариант 1

Вариант 2

Проверьте свои ответы. Поставьте «+» за правильный ответ и «-» за неправильный ответ.

Игра «Шифровка»

Правила игры: На каждую парту раздаётся по карточке с заданием, имеющим код-букву. Выполнив действия и получив результат, записываете код-букву вашей карточки под числом, соответствующим вашему ответу.

В результате получим предложение:

6,8

420

21,6

420

306

65,8

21,6

Подведение итогов урока.

Объявляются оценки за проверочную работу.

Домашнее задание №1301, 1308, 1309

СПАСИБО за внимание!!!

Пример:

Запятая в десятичной дроби отделяет:
1) целую часть от дробной;
2) столько знаков, сколько нулей в знаменателе обыкновенной дроби.

Как перевести десятичную дробь в обыкновенную?

Например, \(0,35\) читается как «ноль целых, тридцать пять сотых». Так и пишем: \(0 \frac{35}{100}\). Целая часть равна нулю, то есть ее можно просто не писать, а дробную часть – сократить на \(5\).
Получим: \(0,35=0\frac{35}{100}=\frac{35}{100}=\frac{7}{20}\).
Еще примеры: \(2,14=2\frac{14}{100}=\frac{214}{100}=\frac{107}{50}\);
\(7,026=7\frac{26}{1000}=\frac{7026}{1000}\).

Этот переход можно делать и быстрее:

Запишите в числитель все число без запятой, а в знаменатель – единицу и столько нулей, столько цифр было отделено запятой.

Звучит сложно, поэтому смотрите картинку:

Как обыкновенную дробь перевести в десятичную?

Для этого надо домножить числитель и знаменатель дроби на такое число, чтобы в знаменателе получилось \(10\), \(100\), \(1000\) и т.д., а потом записать результат в десятичном виде.

Примеры: \(\frac{3}{5}\) \(=\)\(\frac{3\cdot 2}{5\cdot 2}\) \(=\)\(\frac{6}{10}\) \(=0,6\); \(\frac{63}{25}\) \(=\frac{63 \cdot 4}{25\cdot 4}\) \(=\)\(\frac{252}{100}\) \(=2,52\); \(\frac{7}{200}\) \(=\)\(\frac{7 \cdot 5}{200\cdot 5}\) \(=\)\(\frac{35}{1000}\) \(=0,035\).

Этот способ хорошо работает, когда в знаменателе дроби: \(2\), \(5\), \(20\), \(25\)… и т.д., то есть когда сразу понятно, на что надо домножать. Однако в остальных случаях:

Для превращения обыкновенной дроби в десятичную нужно поделить числитель дроби на ее знаменатель.

Например , дробь \(\frac{7}{8}\) проще преобразовать делением \(7\) на \(8\), чем догадываться, что \(8\) можно домножить на \(125\) и получить \(1000\).

Далеко не все обыкновенные дроби без проблем превращаются в десятичные. Точнее, превращаются-то все, но вот записать результат такого превращения бывает весьма трудно. Например, дробь \(\frac{9}{17}\) в десятичном виде будет выглядеть как \(0,52941…\) - и так далее, бесконечный ряд неповторяющихся цифр. Такие дроби обычно оставляют в виде обыкновенных.

Однако некоторые дроби, дающие бесконечный ряд цифр в десятичном виде записаны быть могут. Так происходит в случае, если цифры в этом ряду повторяются. Например, дробь \(\frac{2}{3}\) в десятичном виде выглядит так \(0,66666…\) - бесконечный ряд шестерок. Ее записывают вот так: \(0,(6)\). Содержимое скобки – это как раз и есть бесконечно повторяющаяся часть (так называемый период дроби).

Еще примеры: \(\frac{100}{27}\) \(=\)\(3,7037037037…=3,(703)\).
\(\frac{579}{110}\) \(=5,2636363636…=5,2(63)\).

Виды десятичных дробей:

Сложение и вычитание десятичных дробей

Сложение (вычитание) десятичных дробей выполняется так же, как сложение (вычитание) : главное, чтобы запятая во втором числе стояла под запятой в первом.

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые. Потом сложить количество знаков после запятой в первом числе и во втором, а затем отделить полученное количество знаков в итоговом числе, считая справа налево.

Лучше \(1\) раз посмотреть на картинку, чем \(10\) раз прочитать, поэтому наслаждайтесь:

Деление десятичных дробей

Чтобы разделить десятичную дробь на десятичную дробь, надо перенести запятую во втором числе (делителе) до тех пор, пока оно не станет целым. Потом на столько же перенести запятую в первом числе (делимом). Затем нужно разделить получившиеся числа как обычно. При этом в ответе нужно будет не забыть поставить запятую сразу же, как мы «перейдем за запятую» в делимом.

Снова картинка объяснит принцип лучше любого текста.

На практике бывает легче представлять деление как обыкновенную дробь, потом домножением числителя и знаменателя убирать запятые (или просто сразу передвигать запятые, как делали выше), а затем сокращать получившиеся числа.

\(13,12:1,6=\)\(\frac{13,12}{1,6}\) \(=\)\(\frac{13,12·100}{1,6·100}\) \(=\)\(\frac{1312}{160}\) \(=\)\(\frac{328}{40}\) \(=\)\(\frac{82}{10}\) \(=8,2\).

Пример . Вычислите \(0,0625:(\)\(\frac{1}{8}\) \(+\)\(\frac{5}{16}\) \()\cdot 2,8\).

Решение :

\(0,0625:(\)\(\frac{1}{8}\) \(+\)\(\frac{5}{16}\) \()\cdot 2,8=\)