Случайные события. геометрическая вероятность в пространстве. Распределение Вигнера на фазовом пространстве и отрицательная вероятность
ГЛАВА 1 ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Вероятностный эксперимент. Предмет и задачи теории вероятностей.
Результаты любого эксперимента в той или иной степени зависят от комплекса условий S, при которых данный эксперимент производится. Эти условия либо объективно существуют, либо создаются искусственно (т.е. производится планирование эксперимента).
По степени зависимости результатов эксперимента от условий, при которых он производился, все эксперименты можно разделить на два класса: детерминированные и вероятностные.
o Детерминированные эксперименты- это эксперименты, результаты которых можно предвидеть заранее на основании естественнонаучных законов исходя из данного комплекса условий S.
Примером детерминированного эксперимента является определение ускорения, получаемого телом массы m под воздействием силы F, т.е.. Искомая величина однозначно определяется комплексом условий эксперимента (т.е. массой тела m и силой F).
Детерминированными являются, например, все процессы, основанные на использовании законов классической механики, согласно которым движение тела однозначно определяется заданными начальными условиями и силами, действующими на тело.
o Вероятностные эксперименты (стохастические или случайные)- эксперименты, которые можно повторять произвольное число раз при соблюдении одних и тех же стабильных условий, но, в отличие от детерминированного, исход вероятностного эксперимента неоднозначен, случаен. Т.е. нельзя заранее на основании комплекса условий S предвидеть результат вероятностного эксперимента. Однако, если вероятностный эксперимент повторять многократно при одних и тех же условиях, то совокупность исходов таких экспериментов подчиняется определенным закономерностям. Изучением этих закономерностей (а точнее их математических моделей) и занимается теория вероятностей. Приведем несколько примеров вероятностных экспериментов, которые в дальнейшем будем называть просто экспериментами.
Пример 1
Пусть эксперимент заключается в однократном подбрасывании симметричной монеты. Этот эксперимент может закончиться одним из исключающих друг друга исходов: выпадение герба или решетки (решки). Если точно знать начальные скорости поступательного и вращательного движения и начальное положение монеты в момент броска, то можно предвидеть результат этого эксперимента по законам классической механики. Т.е. он был бы детерминированным. Однако исходные данные эксперимента не могут быть зафиксированными и постоянно изменяются. Поэтому говорят, что результат эксперимента неоднозначен, случаен . Тем не менее, если будем подбрасывать одну и ту же симметричную монету многократно по достаточно длинной траектории, т.е. по возможности сохраним стабильными некоторые условия эксперимента, то совокупное число его исходов подчиняется определенным закономерностям: относительная частота выпадения герба , частоте выпадение бросков (n-число бросков, m 1 -число выпадений герба, m 2 -решки).
Пример 2
Предположим, что мы заполняем карточку спортлото. До проведения тиража выигрышей невозможно предсказать, сколько номеров будет правильно угадано. Однако опыт проведения тиража спортлото говорит о том, что средний процент игроков, угадавших m (1≤m≤6) номеров, колеблется около некоторой постоянной величины. Эти «закономерности» (средний процент правильного угадывания данного количества номеров) используются для расчета фондов выигрыша.
Вероятностные эксперименты имеют следующие общие черты: непредвиденность результата; наличие определенных количественных закономерностей при их многократном повторении при одинаковых условиях; множество возможных исходов.
o Предметом теории вероятностей является количественный и качественный анализ математических моделей вероятностных экспериментов, называемый статической обработкой экспериментальных данных.
o Теория вероятностей- наука, занимающаяся анализом математических моделей для принятия решений в условиях неопределенности.
События и операции над ними.
Относительные частоты и их свойства
Первичным понятием теории вероятностей, неопределяемым через другие понятия, является пространство элементарных исходов Ω. Обычно в качестве пространства элементарных исходов берутся единственно возможные неразложимые результаты эксперимента.
Пример
1. Предположим, что бросается симметричная монета. Тогда (герб и решка).
2. Игральная кость ![]() .
.
3. Бросаются две монеты .
4. Бросаются две игральных кости . Число элементарных исходов 36.
5. На числовой оси w бросается наудачу точка.

6. На бросаются две точки .
 y
y
Определение. Событием называется произвольное подмножество А пространства элементарных исходов Ω. Те элементарные исходы, из которых состоит событие А, называются благоприятствующими событию А.
Говорят, что событие А произошло, если в результате эксперимента происходит элементарный исход w A, т.е. благоприятствующий событию А.
Рассмотрим пример 2. ![]() , –событие, состоящее в выпадении нечетного числа очков; –событие, состоящее в выпадении четного числа очков.
, –событие, состоящее в выпадении нечетного числа очков; –событие, состоящее в выпадении четного числа очков.
o Все пространство элементарных исходов Ω, если взять в качестве события, называют достоверным событием, поскольку оно происходит в любом эксперименте (всегда).
o Пустое множество (т.е. множество, которое не содержит ни одного элементарного исхода) называется невозможным событием, поскольку оно никогда не происходит.
Все остальные события, кроме Ω и , называются случайными.
Операции над событиями
0.1 Суммой событий А и В называется объединение этих множеств А B.
–событие, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий А или В.
0.2 Произведением событий А и В называется пересечение множеств А и В, т.е. А В. Обозначается как АВ.
АВ–событие, когда А и В происходят одновременно.
0.3 Разностью событий А и В называется разность множеств А\В.
А\В–событие, которое происходит <=>, когда происходит А и не происходит В.
o События А и В называются несовместимыми
, если . Если А и В несовместимы, то будем обозначать ![]() .
.
o Говорят, что событие А влечет событие В, если А является подмножеством В, т.е. (когда происходит А, происходит В).
o Событие называется противоположным к событию А.
Пример 2. . происходит тогда, когда А не происходит.
o Говорят, что события Н 1 ,Н 2 ,…,Н n образуют полную группу , если Н 1 +Н 2 +…+Н n =Ω (т.е. Н 1 , Н 2 , Н n –несовместимы, т.е. Н i Н j = , если i≠j).
Например, А и образуют полную группу: .
Предположим, что производится некоторый случайный эксперимент, результат которого описывается пространством Ω. Произведем N экспериментов. Пусть А-некоторое событие (), N(A)-число тех экспериментов, в которых произошло событие А.
Тогда число называется относительной частотой события А.
Аксиомы теории вероятностей
Пусть Ω-пространство элементарных исходов. Предположим, что F-некоторый класс подмножеств Ω.
o Событие-это подмножество Ω, принадлежащее классу F. Любому ставится в соответствие действительное число P(A), называемое вероятностью А , так что при этом выполняется аксиомы:
Аксиома 1.
Аксиома 2. ,т.е. вероятность достоверного события равна 1.
Аксиома 3.
(счетной аддитивности) Если ![]() и
и ![]() , то (для несовместимых событий).
, то (для несовместимых событий).
Элементы комбинаторики
Лемма 1. Из m элементов а 1 ,…,а m первой группы и n элементов b 1 ,…,b n второй группы можно составить ровно m∙n упорядоченных пар вида (а i , b j), содержащих по одному элементу из каждой группы.
Доказательство:

Всего имеем m∙n пар.
Пример. В колоде 4 масти (черва, пика, трефа, бубна), в каждой масти по 9 карт. Итого n=4∙9=36.
Лемма 2. Из n 1 элементов первой группы a 1 , а 2 ,…, а n 1 ,
n 2 элементов второй группы b 1 , b 2 ,…, b n 2 ,
n 3 элементов k-ой группы x 1 , x 2 ,…, x nk
можно составить ровно n 1 ∙ n 2 ∙…∙n k различных упорядоченных комбинаций вида ![]() , содержащих по одному элементу из каждой группы.
, содержащих по одному элементу из каждой группы.
1. При k=2 утверждение выполняется (Лемма 1).
2. Предположим, что Лемма 2 выполняется для k. Докажем для k+1 группы элементов ![]() . Рассмотрим комбинацию
. Рассмотрим комбинацию ![]() как
как ![]() и . Предположение дает возможность вычислить число комбинаций из k элементов, их n 1 n 2 n k . По Лемме 1 число комбинаций из k+1 элементов n 1 n 2 … n k +1 .
и . Предположение дает возможность вычислить число комбинаций из k элементов, их n 1 n 2 n k . По Лемме 1 число комбинаций из k+1 элементов n 1 n 2 … n k +1 .
Пример. При бросании двух игральных костей N=6∙6=36. При бросании трех костей N=6∙6∙6=216.
Геометрические вероятности
Предположим, что на числовой оси имеется некоторый отрезок и на этот отрезок наудачу бросается точка. Найти вероятность того, что эта точка попадет на .
 -геометрическая вероятность на прямой.
-геометрическая вероятность на прямой.
Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Вероятность попадания точки в фигуру g определяется равенством:
 -геометрическая вероятность на плоскости.
-геометрическая вероятность на плоскости.
Пусть в пространстве имеется фигура v, составляющая часть фигуры V. На фигуру V наудачу брошена точка. Вероятность попадания точки в фигуру v определяется равенством:
-геометрическая вероятность в пространстве.
Недостатком классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным числом исходов. Для устранения этого недостатка и вводят геометрические вероятности.
Свойства вероятности
Свойство 1.
Вероятность невозможного события равна 0, т.е. . ![]() .
.
Свойство 2. Вероятность достоверного события равна 1, т.е. , .
Свойство 3.
Для любого события ![]() . , т.к. , то и следовательно .
. , т.к. , то и следовательно .
Свойство 4. Если события А и В несовместимы, то вероятность суммы равна сумме вероятностей:
Случайные величины
o Случайной величиной Х называется функция X(w), отображающая пространство элементарных исходов Ω во множестве действительных чисел R.
Пример. Пусть дважды подбрасывается монета. Тогда .
Рассмотрим случайную величину Х–число выпадений герба на пространстве элементарных исходов Ω. Множество возможных значений случайной величины:2,1,0.
| w | (г,г) | (г,р) | (р,г) | (р,р) |
| X(w) |
Множество значений случайной величины обозначается Ω х. Одной из важных характеристик случайной величины является функция распределения случайной величины.
o Функцией распределения случайной величины Х называется функция F(x) действительной переменной х, определяющая вероятность того, что случайная величина Х примет в результате эксперимента значение, меньшее некоторого фиксированного числа х.
Если рассматривать Х как случайную точку на оси ох, то F(x) с геометрической точки зрения-это вероятность того, что случайная точка Х в результате реализации эксперимента попадет левее точки х.

Простейший поток событий.
Рассмотрим события, которые наступают в случайные моменты времени.
o Потоком событий называют последовательность событий, которые наступают в случайные моменты времени.
Примерами потоков служат: поступление вызовов на АТС, на пункт неотложной медицинской помощи, прибытие самолетов в аэропорт, клиентов на предприятие бытового обслуживания, последовательность отказов элементов и многие другие.
Среди свойств, которыми могут обладать потоки, выделим свойства стационарности, отсутствия последствия и ординарности.
o Поток событий называется стационарным , если вероятность появления k событий за промежуток времени длительности t зависит только от k и t.
Таким образом, свойство стационарности характеризуется тем, что вероятность появления k событий на любом промежутке времени зависит только от числа k и от длительности t промежутка и не зависит от начала его отсчета; при этом различные промежутки времени предполагаются непересекающимися. Например, вероятности появления k событий на промежутках времени (1, 7), (10, 16), (Т, Т+6) одинаковой длительности t=6 единиц времени равны между собой.
o Поток событий называется ординарным ,если за бесконечно малый промежуток времени может появиться не более одного события.
Таким образом, свойство ординарности характеризуется тем, что появление двух и более событий за малый промежуток времени практически невозможно. Другими словами, вероятность появления более одного события в один и тот же момент времени практически равна нулю.
o Говорят, что поток событий обладает свойством отсутствия последствия , если имеет место взаимная независимость появлений того или иного числа событий в непересекающиеся промежутки времени. Таким образом, свойство отсутствия последствия характеризуется тем, что вероятность появления k событий на любом промежутке времени не зависит от того, появились или не появились события в моменты времени, предшествующие началу рассматриваемого промежутка. Другими словами, условная вероятность появления k событий на любом промежутке времени, вычисленная при произвольном предположении о том, что происходило до начала рассматриваемого промежутка (т.е. сколько событий появилось, в какой последовательности), равна безусловной вероятности. Следовательно, предыстория потока не сказывается на вероятности появления событий в ближайшем будущем.
o Поток событий называется простейшим или пуассоновским , если он стационарный, ординарный, без последствия.
o Интенсивностью потока λ называют среднее число событий, которые появляются в единицу времени.
Если постоянная интенсивность потока известна, то вероятность появления k событий простейшего потока за промежуток времени длительности t определяется по формуле:
 ,
, ![]() . Формула Пуассона.
. Формула Пуассона.
Эта формула отражает все свойства простейшего потока, поэтому ее можно считать математической моделью простейшего потока.
Пример. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Найти вероятность того, что за 5 минут поступит: а) два вызова; б) менее двух вызовов; в) не менее двух вызовов. Поток вызовов предполагается простейшим.
По условию λ=2, t=5, k=2. По формуле Пуассона
А) -это событие практически невозможно.
Б) -событие практически невозможно, т.к. события «не поступило ни одного вызова» и «поступил один вызов»-несовместимы.
В) -это событие практически достоверно.
Свойства дисперсии.
Свойство 1. Дисперсия постоянной величины С равна 0.DC=0.
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
Следствие. Дисперсия суммы нескольких независимых случайных величин равна сумме дисперсий этих величин.
Теорема 2.
Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятность появления и непоявления события в одном испытании: ![]() .
.
Случайная величина Х-число появлений события А в n независимых испытаниях. , где Х i -число наступлений событий в i-ом испытании, взаимно независимые, т.к. исход каждого испытания не зависит от исходов остальных.
Т.к. MX 1 =p. , то . Очевидно, что дисперсия остальных случайных величин также равна pq, откуда ![]() .
.
Пример. Проводятся 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию случайной величины X-числа появлений события в этих испытаниях.
n=10; p=0,6; q=0,4.
o Начальным моментом порядка к случайным величинам Х называют математическое ожидание случайной величины Х k:
![]() . В частности, ,
. В частности, , ![]() .
.
Пользуясь этими моментами, формулу для вычисления дисперсии ![]() можно записать так: .
можно записать так: .
Кроме моментов случайной величины Х целесообразно рассматривать моменты отклонения Х-ХМ.
o Центральным моментом порядка k случайной величины Х называют математическое ожидание величины (Х-МХ) k .
В частности
Следовательно, ![]() .
.
Исходя из определения центрального момента и пользуясь свойствами математического ожидания, можно получить формулы:
Моменты более высоких порядков применяются редко.
Замечание. Моменты, определенные выше, называют теоретическими . В отличие от теоретических моментов, моменты, которые вычисляются по данным наблюдений, называют эмпирическими.
Системы случайных величин.
o Вектор , где -случайные величины, называются n-мерным случайным вектором.
Таким образом, случайный вектор отображает пространство элементарных исходов Ω→IR n в n-мерное действительное пространство IR n .
o Функция
Называется функцией распределения случайного вектора или совместной функцией распределения случайных величин .
Свойство 4.
o Случайный вектор называется дискретным , если все его компоненты-дискретные случайные величины.
o Случайный вектор ![]() называется непрерывным
, если существует неотрицательная функция , называется плотностью распределения случайных величин такая, что функция распределения
называется непрерывным
, если существует неотрицательная функция , называется плотностью распределения случайных величин такая, что функция распределения  .
.
Свойства корреляции.
Свойство 1. Абсолютная величина коэффициента корреляции не превосходит единицы, т.е. .
Свойство 2.
Для того чтобы необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью. Т.е. ![]() с вероятностью 1.
с вероятностью 1.
Свойство 3. Если случайные величины независимы, то они некоррелированы, т.е. r=0.
Пусть Х и Y-независимы, тогда по свойству математического ожидания
o Две случайные величины Х и Y называют коррелированными , если их коэффициент корреляции отличен от нуля.
o Случайные величины Х и Y называют некоррелированными если их коэффициент корреляции равен 0.
Замечание. Из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин.
Коэффициент корреляции характеризует тенденцию случайных величин к линейной зависимости. Чем больше по абсолютной величине коэффициент корреляции, тем больше тенденция к линейной зависимости.
o Коэффициентом асимметрии
случайной величины Х называется число 
 Знак коэффициента асимметрии указывает на правостороннюю или левостороннюю асимметрию.
Знак коэффициента асимметрии указывает на правостороннюю или левостороннюю асимметрию.

o Эксцессом случайной величины Х называется число  .
.
Характеризует сглаженность кривой распределения по отношению к кривой нормального распределения.
Производящие функции
o Под целочисленной случайной величиной будем понимать дискретную случайную величину, которая может принимать значения 0,1,2,…
Таким образом, если случайная величина Х-целочисленная, то она имеет ряд распределения
Ее производящей функцией называется функция
Распределение «xи квадрат»
Пусть X i , -нормальные независимые случайные величины, причем математическое ожидании каждой из них равно нулю, а среднее квадратическое отклонение (или дисперсия)-единице. Тогда сумма квадратов этих величин распределена по закону Х 2 с k=n степенями свободы. Если же эти величины Х i связаны одним линейным соотношением, например , то число степеней свободы k=n-1.
Плотность этого распределения  , где
, где  -гамма-функция; в частности, Г(n+1)=n!
-гамма-функция; в частности, Г(n+1)=n!
Отсюда видно, что распределение «x и квадрат» определяется одним параметром-числом степеней свободы k. С увеличением числа степеней свободы распределение медленно приближается к нормальному.
Распределение Стьюдента
Пусть Z-нормально распределенная величина, причем M(Z)=0, G 2 =1, т.е. Z~N(0,1), а V-независимая от Z величина, которая распределена по закону Х 2 с k степенями свободы. Тогда величина имеет распределение, которое называют t-распределением или распределением Стьюдента (псевдоним английского статистика В.Госсета), с k степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному.
Плотность распределения случайной величины t имеет вид  , .
, .
Случайная величина t имеет математическое ожидание Mt=0, (k>2).
Распределение Фишера
Если U и V-независимые случайные величины, распределенные по закону Х 2 со степенями свободы k 1 и k 2 , то величина имеет распределение Фишера F со степенями свободы k 1 и k 2 . Плотность этого распределения  , где
, где
 .
.
Распределение Фишера F определяется двумя параметрами-числами степеней свободы.
Характеристические функции
0. 1 Случайная величина , где i-мнимая единица, т.е. ,а X и Y-действительные случайные величины, называется комплекснозначной случайной величиной. (i 2 = –1).
0. 2 Математическим ожиданием комплекснозначной случайной величины Z называется . Все свойства математического ожидания остаются справедливыми для комплекснозначных случайных величин.
0. 3 Комплекснозначные случайные величины Z 1 =X 1 +iY 1 и Z 2 =X 2 +iY 2 называются независимыми, если независимы соответственно .
Законы больших чисел
Случайные функции
o Случайной функцией называется функция X(t), значение которой при любом значении аргумента t является случайной величиной.
Другими словами, случайной функцией называется функция, которая в результате опыта может принять тот или иной конкретный вид, при этом заранее не известно, какой именно.
o Конкретный вид, принимаемый случайной величиной в результате опыта, называется реализацией случайной функции.
 Т.к. на практике аргумент t чаще всего является временным, то случайную функцию иначе называют случайным процессом.
Т.к. на практике аргумент t чаще всего является временным, то случайную функцию иначе называют случайным процессом.
На рисунке изображено несколько реализаций некоторого случайного процесса.
Если зафиксировать значение аргумента t, то случайная функция X(t) превратится в случайную величину, которую называют сечением случайной функции , соответствующим моменту времени t. Будем считать распределение сечения непрерывным. Тогда Х(t) при данном t определяется плотностью распределения p(x; t).
Очевидно, p(x; t) не является исчерпывающей характеристикой случайной функции X(t), поскольку она не выражает зависимости между сечениями X(t) в разные моменты времени t. Более полную характеристику дает функция ![]() -совместная плотность распределения системы случайных величин
-совместная плотность распределения системы случайных величин ![]() , где t 1 и t 2 -произвольные значения аргумента t случайной функции. Еще более полную характеристику случайной функции X(t) даст совместимая плотность распределения системы трех случайных величин и т.д.
, где t 1 и t 2 -произвольные значения аргумента t случайной функции. Еще более полную характеристику случайной функции X(t) даст совместимая плотность распределения системы трех случайных величин и т.д.
o Говорят, что случайный процесс имеет порядок n , если он полностью определяется плотностью совместимого распределения n произвольных сечений процесса, т.е. системы n случайных величин , где X(t i)-сечение процесса, отвечающее моменту времени t i , но не определяется заданием совместного распределения меньшего, чем n, числа сечений.
o Если плотность совместного распределения произвольных двух сечений процесса вполне его определяет, то такой процесс называется марковским.
Пусть имеется случайная функция X(t). Возникает задача описания ее с помощью одной или нескольких неслучайных характеристик. В качестве первой из них естественно взять функцию ![]() -математическое ожидание случайного процесса. В качестве второй берется среднее квадратическое отклонение случайного процесса .
-математическое ожидание случайного процесса. В качестве второй берется среднее квадратическое отклонение случайного процесса .
 Эти характеристики являются некоторыми функциями от t. Первая из них-это средняя траектория для всех возможных реализаций. Вторая характеризует возможный разброс реализаций случайной функции около средней траектории. Но и этих характеристик недостаточно. Важно знать зависимость величин X(t 1) и X(t 2). Эту зависимость можно характеризовать с помощью корреляционной функции или корреляционного момента.
Эти характеристики являются некоторыми функциями от t. Первая из них-это средняя траектория для всех возможных реализаций. Вторая характеризует возможный разброс реализаций случайной функции около средней траектории. Но и этих характеристик недостаточно. Важно знать зависимость величин X(t 1) и X(t 2). Эту зависимость можно характеризовать с помощью корреляционной функции или корреляционного момента.
Пусть имеются два случайных процесса, по нескольку реализаций которых изображено на рисунках.
У этих случайных процессов примерно одинаковые математические ожидания и средние квадратичные отклонения. Тем не менее это различные процессы. Всякая реализация для случайной функции X 1 (t) медленно меняет свои значения с изменением t, чего нельзя сказать о случайной функции X 2 (t). У первого процесса зависимость между сечениями X 1 (t) и будет больше, чем зависимость для сечений X 2 (t) и второго процесса, т.е. убывает медленнее, чем ![]() , при увеличении Δt. Во втором случае процесс быстрее «забывает» свое прошлое.
, при увеличении Δt. Во втором случае процесс быстрее «забывает» свое прошлое.
Остановимся на свойствах корреляционной функции, которые вытекают из свойств корреляционного момента пары случайных величин.
Свойство 1. Свойство симметричности .
Свойство 2. Если к случайной функции X(t) прибавить неслучайное слагаемое , то от этого корреляционная функция не изменится, т.е. .
Базовые понятия 1 ТВ
Базовые понятия (часть1) по курсу Теория вероятностей
Модель случайного эксперимента.
События (случайные события) и их свойства.
Вероятность и её свойства.
Условная вероятность.
Независимость событий.
Формула полной вероятности.
Формула Байеса.
Модель случайного эксперимента, вероятностное пространство.
Модель такого эксперимента - согласованная тройка объектов (Ω , А ,Р ):
Ω = { ω } - пространство элементарных исходов, совокупность всех возможных элементарных исходов эксперимента. Различные элементарные исходы не пересекаются, они не могут произойти в эксперименте одновременно.
А
= {
А,В,…
}
- класс событий,
полный набор интересующих нас событий.
Каждое событие
– это некоторое подмножество возможных элементарных исходов эксперимента.
Р
-
вероятностная мера
событий
эксперимента.
Для каждого события А
определена его вероятность
Р
(А
), вычисляемая по единому правилу.
Свойства событий:
Полнота класса событий А означает:
А) с каждым событием A мы рассматриваем и его дополнение - событие, состоящее из всех возможных элементарных исходов эксперимента не вошедших в событие А ;
Б) вместе с любыми двумя событиями А
и
В
мы рассматриваем их объединение
 , и пересечение
, и пересечение
 .
.
Следствия:

 называют достоверным
событием, а
называют достоверным
событием, а  называют невозможным
событием.
называют невозможным
событием.
Если = , то события А и В называют несовместными.
Свойства вероятностей:

Способы задания вероятностной меры.
Классическая вероятность . Если
Б) Все элементарные исходы события (элементарные события ), ω А .
В) Вероятности всех элементарных событий равны (равномерная вероятностная мера ), Р (ω ) = 1 / n .
Тогда вероятность любого события А определяется как доля количества элементарных исходов в А (А ) от количества элементарных исходов в Ω . Р (А ) = А ⁄ Ω .
Геометрическая вероятность . Если на пространстве элементарных исходов Ω задана конечная неотрицательная мера s (· ), тогда вероятность любого события А определяется как отношение меры А, s (А ), к мере Ω , s (Ω ). Р (А ) = s (А ) ⁄ s (Ω ).
Плотность распределения. Если
Б) Задана неотрицательная функция р (ω ), (р (ω ) ≥ 0 ), с площадью (s (· )) фигуры V Ω , ограниченной графиком р (ω ) и числовой осью Ω , равной 1 (s (V Ω ) = 1).
А) Функция р (ω ) называется плотностью распределения.
Б) Вероятность любого события А ⊆ Ω задаётся площадью s (V А ) фигуры, ограниченной графиком р (ω ) на части А числовой оси и числовой осью Ω . Р (А ) = s (V А ).
Условная вероятность.
Р В (А )= Р (А В )=[ Р (А В ) ⁄ Р (В )] . При этом 0 ≤ Р В (А ) ≤ 1, т.к. (А В ) ⊆ В и Р (В )>0 .
Независимость событий.
Три события независимы в совокупности,
если:
а) каждые два из них независимы, и
б) объединение каждых двух событий независимо с третьим событием.
Аналогично распространяется понятие независимости в совокупности на большее число событий.
Полная группа событий.
Формула полной вероятности.
Р (А )) = ∑ i [P (Н i )· Р (А Н i )].
Вероятность события можно вычислять как взвешенную сумму условных вероятностей этого события при условии, что происходили события из полной группы событий, где в качестве весовых коэффициентов берутся вероятности соответствующих событий из полной группы.
Формула Байеса.
Р А (Н к ) = (Р (А Н к )) ⁄ (Р (А )) = (Р (А Н к )) ⁄ (∑ i [P (Н i )· Р (А Н i )]).
Типовые модели случайного эксперимента.
Эксперимент с двумя альтернативными событиями - исходами У (успех) и Н (неудача).
Р (У) = p , Р (Н) = q = 1 p .
У(2) . Простейшая Урновая модель .
Извлечение шара из урны с двумя шарами. Модель эквивалентна модели Бернулли В (½).
У(n ) илиR (n ). Классическая Урновая модель .
Извлечение шара из урны с n перенумерованными шарами. Элементарный исход – элементарное событие – номер извлеченного шара. Классическая вероятность с равномерным распределением вероятностей элементарных событий.
У(n
;
m
)
. Урновая модель.
Извлечение шара из урны с m
белыми и (n
–
m
) черными шарами.
Модель эквивалентна модели Бернулли В
(m
/
n
).
Последовательность случайных экспериментов.
У (n *n ). Последовательное извлечение с возвращением двух шаров из урны с n шарами.
У (2 * 2). Последовательное извлечение с возвращением двух шаров из урны с двумя шарами. Модель эквивалентна Биномиальной модели В (2; p ).
У(n *(n -1)). Последовательное извлечение без возвращения двух шаров из урны с n шарами.
Вероятностное пространство - это математическая модель случайного эксперимента (опыта) в аксиоматике А. Н. Колмогорова. Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, необходимую для его математического анализа средствами теории вероятностей. Любая задача теории вероятностей решается в рамках некоторого вероятностного пространства, полностью заданного изначально. Задачи, в которых вероятностное пространство задано не полностью, а недостающую информацию следует получить по результатам наблюдений, относятся к области математической статистики.
Определение
Вероятностное пространство - это тройка , где:
Заметим, что последнее свойство сигма-аддитивности меры эквивалентно (при условии выполнения всех прочих свойств, в том числе конечной аддитивности) любому из следующих свойств непрерывности меры :
Примеры наиболее часто использующихся вероятностных пространств
Дискретные вероятностные пространства
Если множество элементарных исходов конечно или счетно: , то соответствующее вероятностное пространство называется дискретным . В случае дискретных вероятностных пространств событиями обычно считают все возможные подмножества . В этом случае для задания вероятности необходимо и достаточно приписать каждому элементарному исходу число так, чтобы их сумма была равна 1. Тогда вероятность любого события задается следующим образом:
Важным частным случаем такого пространства является классический способ задания вероятностей , когда количество элементарных исходов конечно и все они имеют одинаковую вероятность. Тогда вероятность любого события определяется как отношение его мощности (т.е. количества элементарных исходов, благоприятствующих данному событию) к общему числу элементарных исходов:
.Однако всегда необходимо помнить, что для того, чтобы применять данный способ, необходимо убедиться в том, что элементарные исходы действительно равновероятны. Это должно либо быть сформулировано как исходное условие, либо этот факт следует строго вывести из имеющихся начальных условий.
Вероятностные пространства на прямой
Вероятностные пространства на прямой () естественным образом возникают при изучении случайных величин . При этом в общем случае уже не получается рассматривать в качестве событий любые подмножества прямой, поскольку на таком широком классе обычно нельзя задать вероятностную меру, удовлетворяющую необходимым аксиомам. Универсальная сигма-алгебра событий, достаточная для работы - это сигма-алгебра борелевских множеств : наименьшая сигма-алгебра, содержащая все открытые множества. Эквивалентное определение - наименьшая сигма-алгебра, содержащая все интервалы . Универсальный способ задания вероятностной меры на данной сигма-алгебре - через функцию распределения случайной величины.
Вероятностные пространства в конечномерном пространстве
Вероятностные пространства с множеством элементарных исходов естественным образом возникают при изучении случайных векторов . Универсальной сигма-алгеброй событий при этом также является борелевская сигма-алгебра , порожденная всеми открытыми множествами. Принципиально этот случай мало чем отличается от случая одной прямой.
В науке и практике известны три пути проверки гипотез. Первый состоит в непосредственном (прямом) установлении выдвинутого предположения. Этот метод в криминалистической практике может быть применен к сравнительно небольшой группе предсказательных версий (разыскных и поисковых). Второй путь...(Криминалистика)
Распределения вероятностей и ожидаемая доходность
Как уже не раз говорилось, риск связан с вероятностью того, что фактическая доходность будет ниже се ожидаемого значения. Поэтому распределения вероятностей являются основой для измерения риска проводимой операции. Однако следует помнить, что получаемые при этом оценки носят вероятностный характер. Пример...(Методы принятия управленческих решений)
Качественные и количественные модели оценки вероятности банкротства
Риск дефолта, или кредитный риск, представляет собой риск невыполнения условий кредитного соглашения или рыночной сделки, прежде всего выраженный в неспособности заемщика своевременно и в полном объеме исполнить взятые на себя долговые обязательства (например, в установленный срок выплатить оговоренные...(Финансовый анализ для менеджеров)
Распределение Вигнера на фазовом пространстве и отрицательная вероятность
Даже в нерелятивистской квантовой механике возникают отрицательные вероятности. Здесь нельзя ввести распределение вероятностей (Максвелла) координат х и моментов р, так же, как и в статистической механике. Это невозможно в силу соотношения неопределенности, которое препятствует одновременному измерению...р-адичсское вероятностное пространство
Пусть р : А Qp - мера, определённая на отделимой алгебре А. подмножеств множества 12, которая удовлетворяет условию нормировки /i(12) = 1. Положим Т = Afl и обозначим продолжение меры р на алгебру F символом Р. Тройку (12, J-. Р) называют р-адическим...(КВАНТОВАЯ ФИЗИКА И НЕКОЛМОГОРОВСКИЕ ТЕОРИИ ВЕРОЯТНОСТЕЙ)
РЕГРЕССИЯ. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
Постановка задачи о составлении эмпирических формул Рассмотрим задачу, аналогичную приведенной в параграфе 4.1. Пусть теперь в течение 10 дней в супермаркете проведено исследование зависимости числа посетителей и объема продаж. В этом случае получается некоторый набор пар значений х - числа...(ЧИСЛЕННЫЕ МЕТОДЫ)
Математическое ожидание случайной функции
Рассмотрим случайную функцию X(i). При фиксированном значении аргумента, например при t = tv получим сечение - случайную величину X(t{) с математическим ожиданием M. (Полагаем, что математическое ожидание любого сечения существует.) Таким образом, каждое фиксированное...(ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА)
1. Теория вероятностей изучает эксперименты со случайными исходами.
Эксперимент - это осуществление намеченного действия и результат такого действия.
Результат - это исход эксперимента.
Эксперимент случвйный, если его исход нельзя предсказать до его получения.
Основное ограничение: Мы будем рассматривать только такие эксперименты, которые можно повторять при неизменных условиях неограниченное число раз.
Каждую ситуацию, которую можно наблюдать в зависимости от исхода эксперимента, будем называть событием.
Пример 1.1. Бросаем кость. Исход - то или иное число очков. Событие
Число очков, скажем, больше 3.
Вероятность - степень уверенности в наступлении того или иного события.
Цель теории вероятностей - вычисление вероятностей событий, их комбинаций, а также изучение свойств вероятностей.
2. Теория вероятностей предполагает, прежде всего, построение математической модели случайного эксперимента, которая служит описанием возможных исходов, событий, вероятностей наступления этих событий. Это описание должно быть выполнено таким образом, чтобы обеспечить возможность вычисления вероятностей комбинации событий.
3. Построим модель случайного эксперимента.
Множество исходов случайного эксперимента назовем пространством исходов и обозначим Пространство исходов может быть дискретным или непрерывным.
Пример 1.2. Дискретное пространство: эксперимент - бросание кости, исход - выпадение числа очков, S = {1,2,3,4,5,6}. Непрерывное пространство: эксперимент - ожидание автобуса при условии, что ожидаешь не более минут, исход - конкретное время ожидания,
Событие - любое подмножество пространства исходов Событие обозначим Е.
Событие произошло, если в результате эксперимента исход X принадлежит
Элементарное событие: оно содержит только один исход.
Достоверное событие: оно совпадает с пространством исходов
Невозможное событие: оно совпадает с пустым множеством.
Противоположное событие оно состоит в том, что событие Е не произошло.
Несовместные события: они не имеют общих исходов.
Сумма (или объединение) событий (или ): это событие, заключающееся в том, что из двух событий А и В в результате случайного эксперимента происходит, по крайней мере, одно.
Произведение событий (или ): это событие, заключающееся в том, что события А и В происходят одновременно.
Мы ограничимся наименьшим классом событий, который обладает следующими свойствами:
Пустое множество 0 принадлежит этому классу;
Если событие Е принадлежит классу, то и противоположное событие также принадлежит классу;
Если каждый юменг счетной последовательности событий принадлежит классу, то суммв (объединение) событий также принадлежит классу.
Из последнего свойства вытекает, что и произведение двух событий (или счетного числа событий) принадлежит классу, если каждое событие принадлежит классу.
Класс событий с указанными свойствами достаточен для описвния любого физического явления, возникающего в результате эксперимента. Такой класс событий назовем полем событий
Поле - это множество событий, для которых определены операции сложения и умножения.
Итак, мы ввели где - пространство исходов, поле событий.
Определим вероятность события Р как число, удовлетворяющее следующим свойствам:
Действительное число;
Для любого
(вероятность достоверного события);
Для любой счетной последовательности взаимно несовместимых событий на
Такое достаточно общее определение вероятности позволяет при рассмотрении тех или иных физических явлений конкретизировать понятие вероятности в зависимости от специфики задачи. Итак, вероятность - это функция, заданная на и принимающая значения на .
4. Некоторые свойства вероятностей, вытекающие из определения вероятности.
Свойство
Доказательство.
Но несовместимы. Следовательно, Отсюда,
Свойство
Доказательство.
Несовместимы и Следовательно, Отсюда
5. Конструктивные способы задания вероятностей.
Наиболее трудная задача математического моделирования реальных явлений состоит в правильном задании вероятностей в зависимости от специфики явлен Такое задание должно быть конструктивным, с одной стороны, соответствовать определению вероятности, а с другой стороны - позволять решать конкретную задачу.
5.1. Выполним эксперимент многократно и подсчитаем, сколько раз произошло событие Е. Если - общее число экспериментов, - число экспериментов, в которых произошло событие Е, то назовем относительной частотой появления события Е.
За вероятность примем предел
![]()
5.2. Если - пространство равновозможных несовместных исходов и - число исходов, соответствующих (благоприятствующих) событию Е, то
![]()
где - общее число исходов.
5.3. В том случае, если - непрерывная область, - область, благоприятствующая появлению в результате случайного эксперимента события А, за вероятность удобно принять
где - мера области - мера области
5.4. Пусть А и В два произвольных события. Назовем условной вероятностью отношение
![]()
при условии
События независимы, если
Пример 1.3. В ящике 94 хороших болта и 6 плохих. Из ящика выбраны случайно 5 болтов. Какова вероятность Р, что все выбранные болты хорошие? .
Пример 1.4. Три человека бросают по очереди монету до первого выпадения “орла”. Выигрывает тот, у кого выпадает “орел”. Каковы относительные шансы выигрыша каждого игрока?
Назовем “серией” однократное бросание монеты тремя игроками, начиная с первого. Пусть - вероятность невыпадения "орла” за к серий. Тогда вероятности выигрыша каждого из трех игроков на следующей серии равны (к - произвольное число):
вероятность выигрыша первого игрока
вероятность выигрыша второго игрока
вероятность выигрыша третьего игрока
Следовательно, шансы игроков откосятся как
Пример 1.5. В комнате находятся студенты в количестве человек. Из них курящих - человек, в очках - человек, курящих и в очках - человек. Удаляем случайным образом студента из комнаты. Курит ли он и носит ли он очки?
Теперь предположим, что мы увидели, что удаленный студент в очках. Какова вероятность, что он и курит?
Пример 1.6. Двое решили встретиться в условленном месте между тремя и четырьмя часами дня, причем пришедший ждет партнера не более 20 мин. Какова вероятность встречи?
 Ударение в английском языке
Ударение в английском языке 10 слов с ударением на 1 слог
10 слов с ударением на 1 слог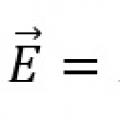 Закон Ома для замкнутой цепи и неоднородного участка цепи
Закон Ома для замкнутой цепи и неоднородного участка цепи