Использование свойств корней при преобразовании иррациональных выражений, примеры, решения. Использование свойств корней при преобразовании иррациональных выражений, примеры, решения Учитель предоставляет свой экран учащемуся
ОТКРЫТЫЙ ДИСТАНЦИОННЫЙ УРОК
по теме: "Преобразование выражений, содержащих квадратные корни".
Учитель математики - Ветохина Антонина Сергеевна
Место работы : ОГКОУ «Школа-интернат № 88 «Улыбка» г. Ульяновск, Ульяновская
область
Предмет: алгебра
Класс: 8
Базовый учебник: « Алгебра 8 класс» : Учебник для общеобразовательных учреждений. Ю.Н. Макарычев, Н.Г.
Миндюк, К.И. Нешков, С.Б. Суворова. - М.: Просвещение, 2011 г
ТДЦ:
Обучающая:
продолжить формирование навыков:
вынесения множителя за знак радикала;
внесения множителя под знак радикала;
разложения на множители;
сокращения дробей;
научить учащегося применять первоначальные знания: свойства корня.
Развивающая : продолжить развитие:
практических умений и навыков;
навыки правильной математической речи;
познавательной деятельности учащегося;
логического мышления учащегося при вычислении в заданиях.
Воспитывающая: продолжить формирование:
культуры общения и культуры ответа на вопросы;
культуры умственного труда;
формировать положительное отношение к предмету, интерес к знаниям.
Тип урока: комбинированный.
Методы обучения : наглядно-словесный, репродуктивный.
Формы организации познавательной деятельности на уроке : самостоятельная и индивидуальная работа.
Оборудование, оформление и техническое оснащение урока:
материалы сайта i-школы « Алгебра - II (8 класс) » ( http://iclass.home-edu.ru );
материалы сайта «ЯКласс» ( http://www.yaklass.ru );
компьютер, мультимедийный проектор.
ПЛАН УРОКА
1. Организационный момент.
2. Актуализация знаний.
3. Физкультминутка для глаз .
4. Изучение нового материала.
5. Физкультминутка двигательная .
6. Закрепление полученных знаний. Практическая работа.
7. Рефлексия. Подведение итогов урока.
8. Домашнее задание.
СТРУКТУРА И ХОД УРОКА
До начала урока, учащийся осуществляет «Вход» на сайт i -школы под своим логином и переходит в курс « Алгебра - II (8 класс) » .
Потом открывает программу Skype для участия в уроке.
| Этап учебного занятия | Задачи этапа | Деятельность учителя | Деятельность учащегося | Ожидаемый результат |
| 1. Организационный момент. 2 мин | Организовать внимание учащегося и готовность к уроку. Раскрыть общие цели урока и плана его проведения Провести релаксацию и дыхательные упражнения. | Учитель приветствует учащегося, спрашивает о настроении и готовности к уроку. Желает совместной плодотворной работы. Сообщает цели и план урока. Просит зайти в закладки: сайт «ЯКласс» предмет 8 класс, в тему III. Функция квадратного корня. Свойства квадратного корня и сделать вкладки занятий 4 и 5 в курсе Алгебра - II (8 класс) » перейти в тему 13 и сделать вкладку урока 26 Соберёмся с силами . В четыре приёма глубоко вдохнём воздух через нос и в пять приёмов с силой выдохнем, задувая воображаемую свечку. Повторим это 2 раза. | Учащийся приветствует учителя. Отвечает на вопросы. Под руководством учителя делает нужные вкладки. Выполняет дыхательные упражнения | Эмоциональный настрой учащегося на урок. Создание доброжелательной атмосферы и делового настроя. Учащийся готов к уроку. |
| 2. Актуализация опорных знаний 1) Проверка домашнего задания. 2 мин 2) Повторение пройденного материала. 6 мин. | Выявить правильность выполнения домашнего задания. Повторить: - свойства квадратных корней | Учитель предоставляет свой экран учащемуся. Открывает выполненную им домашнюю работу. Просит самостоятельно найти ошибки и исправить их, если они имеются. Выключив доступ своего экрана, просит учащегося предоставить доступ своего экран а и перейти на вкладку сайта «ЯКласс» и открыть в занятии 4: Тест «Тренировка по теме: «Свойства квадратных корней» Просит учащегося выключить доступ своего экрана и переходят к физкультминутке. | Принимает замечания или одобрение учителя по выполненному домашнему заданию. Учащийся предоставляет свой экран и, открыв Тест , выполняет его. Учащийся выключает доступ своего экрана. | Проверенное домашнее задание. Учащийся должен: Знать: свойства корней; Уметь: вносить множитель под знак корня, выносить множитель из-под знака корня. |
| 3. Физкультминутка для глаз 2 мин. | Профилактика утомления глаз. | Предлагает учащемуся комплекс упражнений для профилактики утомления глаз. | Снятие напряжения глаз. |
|
| 4. Изучение нового материала 1) Подготовка к изучению
2) Изучение 15 мин. | Организовать деятельность учащегося для получения знаний. Формировать умение самостоятельно изучить новую тему | Учитель просит учащегося предоставить доступ своего экран а и открыть вкладку в курсе « Алгебра - II (8 класс) » : урок 26. Преобразование выражений, содержащих квадратные корни . Просит учащегося выключить доступ экрана и перейти к физкультминутке. | Предоставляет свой экран учителю. Открывает: урок 26 Читает рассмотренные решения примеров, комментируя какие формулы применяются при их решении. Учащийся выключает доступ экрана. | Учащийся готов к получению новых знаний. Учащийся должен иметь представление о преобразовании выражений, содержащих квадратные корни Применять формулы сокращенного умножения. |
| 5. Физкультминутка двигательная 2 мин. | Снять утомление с плечевого пояса и рук | Учитель предлагает учащемуся комплекс упражнений для снятия утомления с плечевого пояса и рук | Учащийся выполняет предложенные упражнения под руководством учителя. | Снятие утомления с плечевого пояса и рук |
| 6. Закрепление полученных знаний. Практическая работа. 6 мин. | Обеспечить понимание учащегося цели, содержания и способов выполнения практических заданий. | Учитель просит учащегося предоставить доступ своего экрана. И для закрепления новой темы, предлагает учащемуся перейти на вкладку сайта «ЯКласс», и открыть в занятии 5: Задания с 1 по 8 . | Учащийся переходит на вкладку сайта «ЯКласс» и открывает в занятии 5 задания ивыполняет их. Потом выключает доступ экрана. | Уметь применять знания на практике. |
| 7. Рефлексия. Подведение итогов урока. 2 мин. | Выявить уровень достижения цели урока. | Учитель оценивает активность работы учащегося на уроке по выполненным заданиям. Задаёт вопросы учащемуся: Что мы изучали на уроке? Чему ты научился на уроке? В чём испытывал затруднения? Учитель объявляет учащемуся оценку, комментируя ее объективность. | Учащийся анализирует свою работу, оценивает её. Рассказывает, что понравилось на уроке, что получалось легко, над чем хотелось бы поработать. | Объективность качественной оценки. |
| 8. Домашнее задание. |
§ 1 Преобразование выражений, содержащих операцию извлечения квадратного корня
Давайте вспомним свойства квадратных корней: если a, b - неотрицательные числа a, b ≥ 0, то справедливы следующие равенства:

Используя эти формулы, можно выполнять различные преобразования выражений, содержащих операцию извлечения квадратного корня, но с условием, что переменные этих выражений принимают только неотрицательные значения. Сделав такое предположение, рассмотрим несколько примеров.
Пример 1: Упросить выражение:
Поскольку в выражении присутствует дробь, для его преобразования воспользуемся вторым свойством:
![]()
Для преобразования знаменателя использовали третье свойство:
В результате первоначальное выражение принимает вид:
Пример 2: Вынести множитель из-под знака квадратного корня:
![]()
При решении примера под буквой А воспользуемся первым и третьим свойствами квадратного корня:
Аналогично преобразуем выражение, представленное в задании под буквой Б:
Пример 3: Внести множитель под знак квадратного корня для
Чтобы внести множитель под знак корня, используем третье свойство справа налево:
![]()
Решим несколько задач по преобразованию выражений, содержащих операцию извлечения квадратного корня, пользуясь формулами сокращенного умножения. Прежде вспомним и выпишем их:
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
a2 - b2 = (a + b)(a - b)
a3 - b3 = (a-b)(a2 + ab + b2)
a3 + a3 = (a + b)(a2 - ab + b2)
Пример 4: Упросить выражение:
Для решения представим число три как квадратный корень из трех в квадрате:
а в знаменателе воспользуемся формулой разности квадратов, тогда получим:

Пример 5: Упростить выражение:
![]()
Для решения, во-первых, рассмотрим выражение:
Если предположить, что
то![]()
используя формулу суммы кубов
Получаем
Сделаем соответствующую замену.
Во-вторых, от операции деления на (a - b) перейдем к операции умножения на обратную дробь:
В-третьих, первую дробь в скобке сократим на выражение:
а затем произведем операцию умножения.
Предположим:
используя формулу разности квадратов, получаем:
![]()
Выражение в числителе первой дроби по формуле квадрата разности можно записать: ![]()
Сделаем соответствующие замены. В числителе и знаменателе первой дроби есть общий множитель, поэтому после сокращения в заключение остается только сложить дроби с одинаковыми знаменателями.
Если знаменатель алгебраической дроби содержит знак квадратного корня, то говорят, что в знаменателе содержится иррациональность. Преобразование выражения к такому виду, чтобы в знаменателе дроби не оказалось знаков квадратных корней, называют освобождением от иррациональности в знаменателе.
§ 2 Алгоритм освобождения от иррациональности в знаменателе дроби
1. Разложить знаменатель дроби на множители;
2. Если знаменатель имеет вид:
Если знаменатель имеет вид:
![]()
или содержит множитель такого вида, то числитель и знаменатель дроби следует умножить соответственно на:
![]()
3. Преобразовать числитель и знаменатель дроби, если возможно, то сократить полученную дробь. Выражения вида:
Рассмотрим, как избавиться от иррациональности в знаменателе на примерах:
А) Преобразуем выражение:
Воспользуемся алгоритмом освобождения от иррациональности в знаменателе дроби: умножим на:
числитель и знаменатель. Получим:

Б) Преобразуем выражение:
В данном примере числитель и знаменатель дроби умножается на сопряженное выражение:
Итак, мы разобрали несколько примеров на упрощение выражений, содержащих квадратные корни.
Список использованной литературы:
- Мордкович А.Г. «Алгебра» 8 класс. В 2 ч. Ч.1Учебник для общеобразовательных учреждений / А.Г. Мордкович. – 9-е изд., перераб. – М.: Мнемозина, 2007. – 215с.: ил.
- Мордкович А.Г. «Алгебра» 8 класс. В 2 ч. Ч.2 Задачник для общеобразовательных учреждений / А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская. – 8-е изд., – М.: Мнемозина, 2006. – 239с.
- Алгебра. 8 класс. Контрольные работы для учащихся образовательных учреждений Л.А. Александрова под ред. А.Г. Мордковича 2-е изд., стер. - М.: Мнемозина, 2009. - 40с.
- Алгебра. 8 класс. Самостоятельные работы для учащихся образовательных учреждений: к учебнику А.Г. Мордковича, Л.А. Александрова под ред. А.Г. Мордковича. 9-е изд., стер. - М.: Мнемозина, 2013. - 112с.
Разделы: Математика
Цели урока:
- Повторить определение арифметического квадратного корня, свойства арифметического квадратного корня.
- Обобщить и систематизировать знания учащихся по этой теме.
- Закрепить навыки и умения решения примеров на тождественные преобразования выражений, содержащих арифметические квадратные корни.
- Дать возможность каждому ученику как можно более полно раскрыть свои возможности.
- Расширять кругозор и познакомить учащихся с математиками средних веков.
Тип урока: урок-практикум.
Оборудование урока: раздаточный материал, цветной мел, графопроектор, портрет Рене Декарта, плакаты с формулами.
Ход урока
I. Организационный момент.
Тема нашего урока «Преобразование выражений, содержащих арифметические квадратные корни». Сегодня на уроке мы будем повторять правила преобразования выражений, содержащих квадратные корни. Это и преобразование корней из произведения, дроби и степени, умножение и деление корней, вынесение множителя за знак корня, внесение множителя под знак корня, приведение подобных слагаемых и освобождение от иррациональности в знаменателе дроби.
II. Устный опрос по теории.
- Дайте определение арифметического квадратного корня. (Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а ).
- Перечислите свойства арифметического квадратного корня. (Арифметический квадратный корень из произведения неотрицательных множителей равен произведению корней из этих множителей. Арифметический квадратный корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, делённому на корень из знаменателя ).
- Чему равно значение арифметического квадратного корня из х 2 ? (|х | ).
- Чему равно значение арифметического квадратного корня из х 2 , если х≥0? х<0? (х. –х ).
III. Устная работа. (Записано на доске).
Найдите значение корня: |
|
Найдите значение выражения: |
|
Внесите множитель под знак корня: |
|
Сравните: |
|
IV. Отработка знаний по данной теме. (На партах у каждого листок с заданиями ).
1. Выполните действия.
- Как будем решать примеры а и б? (Раскроим скобки, приведём подобные слагаемые ).
- Как будем решать примеры в и г? (Применим формулу разности квадратов ).
- Как будем решать примеры д и е? (Вынесем множитель за знак корня и приведём подобные слагаемые ).
2 + 0,3- 4 + 0,01 |
|||||||||
3 + 0,5 - 2 + 0,01 |
(Ученики по вариантам выполняют примеры в тетрадях, 6 учеников по 1 примеру решают у задней доски ).
– Проверка через графопроектор. Каждому ответу соответствует определённая буква. В результате получаются слово: Декарт.
V. Историческая справка.
Ученик выступает с небольшим сообщением.
В 1626 году нидерландский математик А.Ширар ввел близкое к современному обозначение корня V. Если над этим знаком стояла цифра 2, то это означало корень квадратный, если 3 – кубический. Это обозначение стало вытеснять знак Rx. Однако долгое время писали Vа+в с горизонтальной чертой над суммой. Лишь в 1637 году Рене Декарт соединил знак корня с горизонтальной чертой, применив в своей «Геометрии» современный знак корня . Этот знак вошёл во всеобщее употребление лишь в начале XVIII века. (На доске – портрет Рене Декарта, рисунок ).
VI. Отработка знаний по теме.
2. Разложите на множители.
а и б – разложим по формуле разности квадратов, в и г – используя определение арифметического квадратного корня, заменим 7 и 13 квадратами из квадратных корней, а потом вынесем за скобки общий множитель ).
а) а – 9, а≥0 |
||||
б) 16 – в, в≥0 |
||||
Ученики решают в тетрадях по вариантам, 2 человека (по одному от каждого варианта) решают у доски.
– Проверка.
3. Сократите дробь.
– Как будем выполнять это задание? (Разложим на множители или числитель, или знаменатель, а потом сократим ).
Ученики решают в тетрадях по вариантам, 4 человека решают у доски. Примеры д и е решают дополнительно, кто успеет.
– Проверка.
4. Освободитесь от иррациональности в знаменателе дроби.
– Что будем делать в этом задании? (Преобразуем дробь так, чтобы знаменатель не содержал квадратного корня: а и б будем домножать и числитель, и знаменатель на квадратный корень, записанный в знаменателе; в и г будем домножать на сумму или разность выражения, записанного в знаменателе для того, чтобы получилась разность квадратов ).
Ученики решают по вариантам, 2 человека решают по 2 примера у доски.
– Проверка.
VII. Написание теста.
У каждого на парте листок с заданиями теста (приложение 1 ). Подписали листок и выполнили задания в этом же листке. После написания работы сдали, проверили ответы и разобрали, почему так, через графопроектор.
VIII. Домашнее задание. с. 109 № 503 (а–г), 504.
Материал этой статьи стоит рассматривать как часть темы преобразование иррациональных выражений . Здесь мы на примерах разберем все тонкости и нюансы (которых немало), возникающие при проведении преобразований на базе свойств корней.
Навигация по странице.
Вспомним свойства корней
Коль скоро мы собрались разбираться с преобразованием выражений с использованием свойств корней, то не помешает вспомнить основные , а еще лучше записать их на бумагу и расположить перед собой.
Сначала изучаются квадратные корни и следующие их свойства (a , b , a 1 , a 2 , …, a k - действительные числа):
А позже представление о корне расширяется, вводится определение корня n-ой степени, и рассматриваются такие свойства (a , b , a 1 , a 2 , …, a k - действительные числа, m , n , n 1 , n 2 , ..., n k - натуральные числа):
Преобразование выражений с числами под знаками корней
По обыкновению сначала учатся работать с числовыми выражениями, а уже после этого переходят к выражениям с переменными. Так поступим и мы, и сначала разберемся с преобразованием иррациональных выражений, содержащих под знаками корней только числовые выражения, а уже дальше в следующем пункте будем вводить под знаки корней и переменные.
Как это может быть использовано для преобразования выражений? Очень просто: например, иррациональное выражение мы можем заменить выражением или наоборот. То есть, если в составе преобразовываемого выражения содержится выражение, совпадающее по виду с выражением из левой (правой) части любого из перечисленных свойств корней, то его можно заменить соответствующим выражением из правой (левой) части. В этом и состоит преобразование выражений с использованием свойств корней.
Приведем еще несколько примеров.
Упростим выражение ![]() . Числа 3
, 5
и 7
положительные, поэтому мы можем спокойно применять свойства корней. Здесь можно действовать по-разному. Например, корень на базе свойства можно представить как , а корень с использованием свойства при k=3
- как , при таком подходе решение будет иметь такой вид:
. Числа 3
, 5
и 7
положительные, поэтому мы можем спокойно применять свойства корней. Здесь можно действовать по-разному. Например, корень на базе свойства можно представить как , а корень с использованием свойства при k=3
- как , при таком подходе решение будет иметь такой вид:
Можно было поступить иначе, заменив на , и дальше на , в этом случае решение выглядело бы так:
Возможны и другие варианты решения, например, такой:
Разберем решение еще одного примера. Преобразуем выражение . Взглянув на список свойств корней, выбираем из него нужные нам свойства для решения примера, понятно, что здесь пригодятся два из них и , которые справедливы для любых a
. Имеем:
Как вариант, сначала можно было преобразовать выражения под знаками корней с использованием 
а уже дальше применять свойства корней
До этого момента мы преобразовывали выражения, которые содержат только квадратные корни. Пришло время поработать с корнями, имеющими другие показатели.
Пример.
Преобразуйте иррациональное выражение  .
.
Решение.
По свойству ![]() первый множитель заданного произведения можно заменить числом −2
:
первый множитель заданного произведения можно заменить числом −2
:
Идем дальше. Второй множитель в силу свойства ![]() можно представить как , а 81
не помешает заменить четверной степенью тройки, так как в остальных множителях под знаками корней фигурирует число 3
:
можно представить как , а 81
не помешает заменить четверной степенью тройки, так как в остальных множителях под знаками корней фигурирует число 3
:
Корень из дроби целесообразно заменить отношением корней вида , которое можно преобразовать и дальше:  . Имеем
. Имеем
Полученное выражение после выполнения действий с двойками примет вид ![]() , и остается преобразовать произведение корней.
, и остается преобразовать произведение корней.
Для преобразования произведений корней их обычно приводят к одному показателю, в качестве которого целесообразно брать показателей всех корней. В нашем случае НОК(12, 6, 12)=12
, и к этому показателю придется приводить лишь корень , так как остальные два корня уже имеют такой показатель. Справиться с этой задачей позволяет равенство , которое применяют справа налево. Так ![]() . Учитывая этот результат, имеем
. Учитывая этот результат, имеем
Теперь произведение корней можно заменить корнем произведения и выполнить остальные, уже очевидные, преобразования:
Оформим краткий вариант решения:
Ответ:
 .
.
Отдельно подчеркнем, что для применения свойств корней необходимо учитывать ограничения, наложенные на числа под знаками корней (a≥0 и т.п.). Их игнорирование может спровоцировать возникновение неверных результатов. Например, мы знаем, что свойство имеет место для неотрицательных a . На его основе мы спокойно можем перейти, к примеру, от к , так как 8 – положительное число. А вот если взять имеющий смысл корень из отрицательного числа, например, , и на базе указанного выше свойства заменить его на , то мы фактически заменим −2 на 2 . Действительно, , а . То есть, при отрицательных a равенство может быть и неверным, как могут быть неверными и другие свойства корней без учета оговоренных для них условий.
Но сказанное в предыдущем пункте вовсе не означает, что выражения с отрицательными числами под знаками корней невозможно преобразовывать с использованием свойств корней. Их просто предварительно нужно «подготовить», применив правила действий с числами или воспользовавшись определением корня нечетной степени из отрицательного числа, которому соответствует равенство ![]() , где −a
– отрицательное число (при этом a
– положительное). Например, нельзя сразу заменить на , так как −2
и −3
– отрицательные числа, но позволяет нам от корня перейти к , и уже дальше применять свойство корня из произведения:
, где −a
– отрицательное число (при этом a
– положительное). Например, нельзя сразу заменить на , так как −2
и −3
– отрицательные числа, но позволяет нам от корня перейти к , и уже дальше применять свойство корня из произведения: ![]() . А в одном из предыдущих примеров переходить от корня к корню восемнадцатой степени нужно было не так
. А в одном из предыдущих примеров переходить от корня к корню восемнадцатой степени нужно было не так ![]() , а так
, а так ![]() .
.
Итак, для преобразования выражений с использованием свойств корней, надо
- выбрать подходящее свойство из списка,
- убедиться, что числа под корнем удовлетворяют условиям для выбранного свойства (в противном случае требуется выполнить предварительные преобразования),
- и провести задуманное преобразование.
Преобразование выражений с переменными под знаками корней
Для преобразования иррациональных выражений, содержащих под знаком корня не только числа, но и переменные, свойства корней, перечисленные в первом пункте этой статьи, приходится применять аккуратно. Связано это по большей части с условиями, которым должны удовлетворять числа, участвующие в формулах. Например, опираясь на формулу , выражение можно заменить выражением лишь для таких значений x , которые удовлетворяют условиям x≥0 и x+1≥0 , так как указанная формула задана для a≥0 и b≥0 .
Чем опасно игнорирование этих условий? Ответ на этот вопрос наглядно демонстрирует следующий пример. Допустим, нам нужно вычислить значение выражения при x=−2
. Если сразу подставить вместо переменной x
число −2
, то получим нужное нам значение ![]() . А теперь представим, что мы, исходя из каких-то соображений, преобразовали заданное выражение к виду , и только после этого решили вычислить значение. Подставляем вместо x
число −2
и приходим к выражению
. А теперь представим, что мы, исходя из каких-то соображений, преобразовали заданное выражение к виду , и только после этого решили вычислить значение. Подставляем вместо x
число −2
и приходим к выражению ![]() , которое не имеет смысла.
, которое не имеет смысла.
Давайте проследим, что происходит с областью допустимых значений (ОДЗ) переменной x
при переходе от выражения к выражению . ОДЗ мы упомянули не случайно, так как это серьезный инструмент контроля допустимости проделанных преобразований, и изменение ОДЗ после преобразования выражения должно как минимум насторожить. Найти ОДЗ для указанных выражений не составляет труда. Для выражения ОДЗ определяется из неравенства x·(x+1)≥0
, его решение дает числовое множество (−∞, −1]∪∪}
 Ударение в английском языке
Ударение в английском языке 10 слов с ударением на 1 слог
10 слов с ударением на 1 слог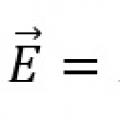 Закон Ома для замкнутой цепи и неоднородного участка цепи
Закон Ома для замкнутой цепи и неоднородного участка цепи